线性回归&Logistic Model

线性回归模型​​，它是统计学和机器学习中最基础、最核心的预测模型之一，主要用于解决​​回归问题​​，即预测一个​​连续的数值型输出​​。

核心思想：建立“输入”与“输出”之间的线性关系

线性回归的核心目标非常直观：​​假设并建模目标变量 y（因变量、输出）与一个或多个预测变量 x（自变量、特征、输入）之间存在的线性关系。​​

它试图找到一条（简单线性回归）或一个平面/超平面（多元线性回归）来“最佳”拟合数据点，从而当我们知道 x 的值时，就可以基于这条线/平面预测 y 的值。

模型表示

1. ​​简单线性回归：​​
   • 只涉及​​一个​​预测变量 x 和一个目标变量 y。
   • ​​模型方程：​​ y = β₀ + β₁ * x + ε
     • y: ​​目标变量​​ (Dependent/Target Variable) - 我们要预测的连续值（例如：房价、销售额、温度）。
     • x: ​​预测变量​​ (Independent/Predictor Variable/Feature) - 我们用来做预测的变量（例如：房屋面积、广告投入、时间）。
     • β₀: ​​截距​​ (Intercept) - 当 x = 0 时，直线与 y 轴相交的点（预测值）。它代表了模型中所有输入特征都为 0 时的基准预测值（注意：这个值本身可能没有实际物理意义）。
     • β₁: ​​斜率/系数​​ (Slope/Coefficient) - ​​表示 x 每增加（或减少）一个单位时，y 平均预期会相应增加（或减少）的量。​​ 这是理解 x 对 y ​​影响方向和大小​​的关键。β₁ > 0 表示正相关（x 增大，y 增大）；β₁ < 0 表示负相关（x 增大，y 减小）。
     • ε: ​​误差/残差​​ (Error/Residual) - 模型无法完美解释的部分。它代表了实际观测值 y 与模型预测值 ŷ = β₀ + β₁ * x 之间的随机差异。这是由未包含在模型中的变量、测量误差或数据本身的随机性引起的。
2. ​​多元线性回归：​​
   • 涉及​​多个​​预测变量 x₁, x₂, ..., xₚ 来预测一个目标变量 y。
   • ​​模型方程：​​ y = β₀ + β₁*x₁ + β₂*x₂ + ... + βₚ*xₚ + ε
     • y: 目标变量。
     • x₁, x₂, ..., xₚ: ​​多个预测变量​​。
     • β₀: 截距。
     • β₁, β₂, ..., βₚ: ​​每个预测变量对应的斜率/系数​​。​​βⱼ 的解释为：在保持模型中其他所有预测变量不变的前提下，xⱼ 每变化一个单位，y 平均预期会发生的变化量。​​ 理解这种"保持其他变量不变"的条件对于避免混淆​​关联性​​和​​因果性​​至关重要。
     • ε: 误差项。

线性回归的“学习”过程就是寻找最优的系数 β₀, β₁, ..., βₚ，使得模型拟合数据的效果最好。这个“最好”的标准通常是：

• ​​最小二乘法：​​
  • ​​目标：​​ 找到一组系数，使得模型对所有训练样本的​​预测值 ŷᵢ​​ 和 ​​实际观测值 yᵢ​​ 之间的​​平方误差和​​最小化。
  • ​​损失函数：​​ Sum of Squared Residuals = Σᵢ(yᵢ - ŷᵢ)² = Σᵢ(εᵢ)²。
  • ​​几何意义：​​ 在二维图中，就是找一条直线，使得所有数据点到这条直线的​​垂直距离（残差）的平方和最小​​。
  • ​​求解：​​ 对于普通最小二乘法 (Ordinary Least Squares, OLS)，可以通过求导找到解析解（数学公式直接计算），也可以通过梯度下降等优化算法迭代求解（尤其是特征非常多或者涉及正则化时）。

拟合完模型后，我们需要评估它的好坏，并检查是否满足基本假设：

1. ​​拟合优度：​​
   • ​​R² (决定系数)：​​ 最常用的指标之一。表示模型解释的目标变量 y 的总变异比例。范围在 0 到 1 之间（有时会是负数，表示模型比简单均值预测还差）。​​R² = 1 - (SS_res / SS_tot)​​，其中 SS_res 是残差平方和，SS_tot 是总平方和。越接近 1，表示模型拟合数据越好（解释变异比例越大）。
   • ​​调整 R²：​​ 对 R² 的修正，考虑了模型中特征个数的影响。在比较包含不同数量特征的模型时，调整 R² 比 R² 更公平。
   • ​​均方根误差 (RMSE) / 均方误差 (MSE)：​​ 直接衡量预测值 ŷ 与实际值 y 的平均偏差大小。MSE 是残差平方和的平均值，RMSE 是 MSE 的平方根。单位和 y 相同，数值越小越好。

​​Logistic 回归​​。

虽然名字里有“回归”，但它​​本质上是一种非常经典的用于解决 分类 问题的统计学习方法​​，尤其是在二分类问题中应用极为广泛。它的核心思想是​​基于输入特征来预测样本属于某个类别的概率​​。

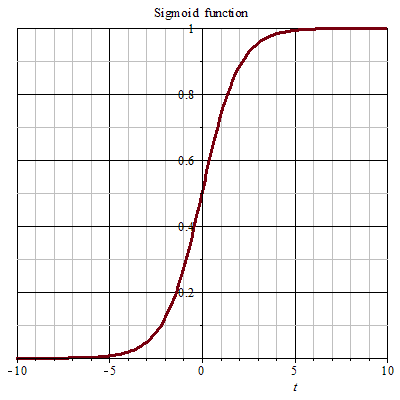
$$ sigmoid(x) = \frac{\mathrm{1} }{\mathrm{1} + e^{-x} } $$

核心概念解析

1. ​​目标是分类：​​
   • 最终输出是一个​​类别标签​​（例如：是/否、垃圾邮件/非垃圾邮件、患病/健康、违约/不违约）。
   • 最常见的应用场景是​​二分类​​。但通过扩展（例如 One-vs-Rest 或 Softmax），也可以用于多分类。
2. ​​概率基础：​​
   • Logistic 回归的核心不是直接预测类别标签，而是预测某个样本属于“正类”（通常标记为 1，例如“是”、“患病”）的​​概率​​。
   • 模型的输出是一个介于 ​​0 和 1 之间​​的概率值。​​0.5​​ 通常作为决策边界：
     • 如果预测概率 >= 0.5，则判定为正类 (1)。
     • 如果预测概率 < 0.5，则判定为负类 (0)。（阈值可根据实际需求调整）
3. ​​Logistic 函数（Sigmoid 函数）：​​
   • ​​核心转换器：​​ Logistic 回归的核心在于它将线性回归模型 z 的输出，通过一个称为 ​​Logistic 函数​​或 ​​Sigmoid 函数​​的非线性函数，映射到 (0, 1) 区间内。
   • ​​函数形式：​​
     σ(z) = 1 / (1 + e^(-z))
     • z 是线性模型的输出：z = β₀ + β₁x₁ + β₂x₂ + ... + βₚxₚ
     • ​​S 形曲线：​​
       • 当 z 非常大（趋于正无穷）时，σ(z) 趋近于 ​​1​​。
       • 当 z 非常小（趋于负无穷）时，σ(z) 趋近于 ​​0​​。
       • 当 z = 0 时，σ(z) = 0.5。
     • ​​作用：​​ 这个 S 形曲线完美地将任何实数值 z 平滑地压缩到了 (0, 1) 区间，使其成为一个有效的概率估计（P(Y=1 | X)）。
4. ​​模型结构：​​
   • ​​线性部分：​​ 首先，模型计算特征的​​线性加权和​​：z = β₀ + β₁x₁ + β₂x₂ + ... + βₚxₚ
     • β₀: 截距项（也叫偏置项）。
     • β₁, β₂, ..., βₚ: 对应于每个特征 x₁, x₂, ..., xₚ 的​​系数​​（权重），反映了该特征对结果预测的影响力大小和方向（正系数增加概率，负系数降低概率）。
   • ​​非线性转换：​​ 将线性组合 z 输入 Sigmoid 函数，得到预测概率：P(Y=1 | X) = σ(z) = 1 / (1 + e^-z)
   • 这个 P(Y=1 | X) 就是模型对给定输入 X 下样本属于正类 (1) 的概率估计。

如何“学习”（训练模型）

目标是找到最优的系数 β₀, β₁, ..., βₚ，使得模型预测的概率尽可能接近样本的真实标签。

1. ​​定义损失函数：​​
   • Logistic 回归使用 ​​二元交叉熵损失​​ 或 ​​对数损失​​。这个损失函数专门设计用于衡量预测概率分布与真实分布之间的差异，尤其适合衡量概率输出。
   • ​​损失函数公式（简化形式）：​​
     Loss = - [ y * log(p) + (1 - y) * log(1 - p) ]
     • y 是真实标签（0 或 1）。
     • p 是模型预测该样本属于正类的概率 (P(Y=1 | X))。
   • ​​逻辑：​​
     • 如果真实标签 y=1，损失为 -log(p)。预测概率 p 越接近 1，损失越小（趋近于 0）。
     • 如果真实标签 y=0，损失为 -log(1 - p)。预测概率 p 越接近 0，损失越小（趋近于 0）。
     • 预测越离谱 (e.g., y=1 但 p 接近 0)，损失越大。
2. ​​优化：​​
   • 模型的训练过程就是​​最小化所有训练样本上的总损失（或平均损失）​​。
   • 这个最小化过程通常使用​​梯度下降​​或其变体（如随机梯度下降、Mini-batch 梯度下降）来求解。梯度下降通过计算损失函数关于每个系数 β 的梯度（偏导数），并沿梯度相反方向（即下降最快的方向）不断更新系数，逐步逼近最优解（使总损失最小）。
   • 有时会加入​​正则化项​​（如 L1 或 L2 正则化）到损失函数中，以控制模型复杂度，防止过拟合。