1.签到题
答案的第一位是1
second number is eight
叁:9
最后一个是八
第一题:1 8 9 8(北京大学的创校时间xD),这读完都知道在哪吧……
2.小北问答
1某厂的CPU采用了大小核架构,大核有超线程,小核没有超线程。已知物理核心数为12,逻辑核心数为16,大核数量为____,小核数量为____。
都说了鸡兔同笼嘛,Ez
x+y=12
2x+y=16
x=4 y=8
2 C语言中,假设有函数 void f(const void **p);,我们有 void **q;,请问不使用强制类型转换,直接调用 f(q) 是否符合 C 的规范?
虽然这学期学了C语言,我的感觉是不符合,const是不能改的指针?
3 ARM架构的sve2指令集具有可变向量长度,且无需重新编译代码,就可以在不同向量长度的硬件上运行。sve2指令集的最小硬件向量长度是____,最大硬件向量长度是____。
fp4 是一种新的数字格式,近期发布的许多硬件都增加了对 fp4 的支持。SE2M1(一位符号,两位 exponent,一位 mantissa)条件下,fp4 能精确表示的最大数字是____,能精确表示的最小的正数是____。
虽然很常听到,但是却没实际了解过,看到这篇文章:
https://www.cnblogs.com/lemonzhang/p/17843336.html

跟着规则简单算一下:
1.1*2^expo=1.1*2^1
1.1二进制计算为1.5
1.5*2=3
1.5*2^-2=0.375
好吧,算的不对,找gpt咯
![O3KYG}ZCK2EZ0BH]QNM59Q1.png](https://blog.muwinds.com/wp-content/uploads/2025/01/202501261737821728211170.png)
5. 储存
(填写字母,字母之间不要空格)
ZNS(Zoned Namespaces)SSD是一种新型储存设备,关于传统SSD与ZNS(Zoned Namespaces)SSD的行为差异,以下哪些说法是正确的?(多选)
A. 当写入一个已有数据的位置时,传统SSD会直接原地覆盖,而ZNS SSD必须先执行Zone Reset操作
B. 传统SSD的FTL会维护逻辑地址到物理地址的映射表,而ZNS SSD可以显著简化或消除这个映射过程
C. 当可用空间不足时,传统SSD会自动触发垃圾回收,而ZNS SSD需要主机端主动管理并执行显式擦除
D. 传统SSD一般支持任意位置的随机读取,而ZNS SSD只支持顺序读取
E. 传统SSD通常需要较大比例的预留空间(Over-Provisioning),而ZNS SSD可以将这部分空间暴露给用户使用
ZNS确实是第一次接触的概念
跟着画饼文档快速猜一下?

能推出来A是对的,ZNS提到由于数据不会被不断地重写,因此提高了耐久度
B也是对的,管理传入数据缓存和逻辑到物理映射需要大量数据
C也是对的,垃圾收集说了
D没说,但是感觉应该错,不然SSD干啥……
E也提到了,是对的
A B C E
十发交到最后这个题都没改对 我佛了
6. OpenMPI
(填写patter为x.y.z,版本号的前缀v省略)
OpenMPI 是一个开源的消息传递接口 (MPI) 实现,在高性能计算领域被广泛使用。截至2025年1月18日,OpenMPI 发布的最新稳定版本为 _____,在此版本的 OpenMPI中内置使用的 PRRTE 的版本为 _____。大家可以了解一下PRRTE的作用,OpenMPI 4 到 5 的架构变化,还挺有趣的。
上官网查我还不会?
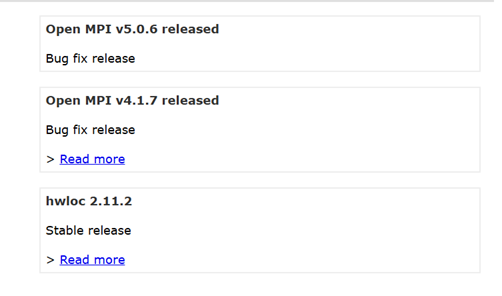
![YSWU9@1TJF2}2WH0MY67Z]Q.png](https://blog.muwinds.com/wp-content/uploads/2025/01/202501261737821812177851.png)
5.0.6 3.0.7
RDMA 是一种高性能网络通信技术,它允许计算机直接访问远程内存,从而大大降低了通信延迟和 CPU 开销。目前,主流的 RDMA 实现包括 InfiniBand、RoCE、RoCEv2 和 iWARP。下图中从左到右的四列展示了四种 RDMA 实现的架构图,请你说出按照从左到右的顺序,说出下图中的四列分别对应了什么 RDMA 的实现架构_____。
A: RoCE B: RoCEv2 C: iWARP D: InfiniBand
前几天讲座说过这个(如果不是前几天的 北大linux俱乐部B站号肯定也有,看到这个图我都恢复记忆了xD)
![)@57]LM}O~405WBXOVJ({6G.png](https://blog.muwinds.com/wp-content/uploads/2025/01/202501261737821939485408.png)
8. HPCKit
(填数字序号,数字之间不要空格)
HPCKit 是针对鲲鹏平台深度优化的HPC基础软件,请选择以下组件的具体作用。
A. BiSheng B. HMPI C. KML D. KBLAS E. EXAGEAR
选项:
1. 高性能数学计算加速库
2. 基础线性代数过程库
3. 高性能通信库
4. X86到ARM的二进制指令动态翻译软件
5. 编译器套件
编译器套件选A,之前折腾openEuler的时候看到过
https://docs.openeuler.org/zh/docs/20.03_LTS_SP3/docs/thirdparty_migration/bisheng.html
高性能通信库,我看HMPI的名字就比较像通信用的,B
KML我还真不知道,谷歌一下才知道是高性能数学加速库
KBLAS,感觉是数学的,已经选了一个那就是线性代数咯?
EXAGEAR不说了,就剩一个了,猜都猜出来了。
53124
9. CXL
(填数字,保留两位有效数字)
在传统的AI/ML计算中,模型训练和推理通常涉及大量的数据传输,尤其是在需要在CPU和GPU之间频繁交换数据时。例如,一个深度学习模型的训练任务可能包含以下步骤:
1. 数据加载和预处理在CPU上完成。
2. 预处理后的数据从CPU传输到GPU进行训练计算。
3. 训练完成后,模型更新结果传回CPU进行后续处理。
假设有以下条件:
• 每次批处理需要传输的数据量为1GB。
• GPU每秒钟可以完成10次这样的批处理。
• 传统架构下,CPU到GPU的PCIe传输延迟为50μs,传输带宽为10GB/s。
• CXL架构下,传输延迟降至10μs,且数据访问可直接完成,无需显式传输。
假设总训练任务包含10000次批处理。比较传统架构和CXL架构下完成任务所需的总时间,计算加速比(传统架构时间 / CXL架构时间),保留两位有效数字。
(该题基于理想化模型,与真实情况并非完全符合)
传输要0.1s,延迟50us,0.1s的gpu批处理
0.00000005s,算了直接忽略吧,反正只让保留两位小数
CXL传输速度快在加个0.1s就行,算出来差不多2.00?
10. 量子计算
(填数字,小数形式)
量子计算是一种基于量子力学原理的计算方式,它利用量子比特的叠加态和纠缠态来进行计算,被认为是下一代计算技术。加速量子计算的模拟、数据处理等负载也是目前高性能计算领域的热点之一。
初始状态为∣0⟩∣0⟩的量子比特,经过一次Hadamard门(H门)操作后,测量得到∣0⟩∣0⟩的概率是______?经过两次Hadamard门(H门)操作后,测量得到∣0⟩∣0⟩的概率是______?
这个是真跪了,从来没了解过,直接GPT了,生病了真写不动。

问题C:不简单的编译
【提示:只要是算卷积算出来的都可以,不能去hack结果校验过程。算法什么的都可以换,但预期解不需要这么做。本题分值为100分,可以尝试简单方法】
众所周知,HPC领域中常用的、性能比较好的语言有 C, C++, Fortran。这些语言常用的编译器有五款,其中 AMD, Intel, NVIDIA 御三家各维护了一款编译器,而开源社区维护了 GNU 和 LLVM 两款编译器。
现在有这么一个涉及了三种语言的计算卷积的小项目(见附件)
handout/ ├── CMakeLists.txt ├── filter.F90 └── main.cpp
使用合适的编程语言、编译器、编译选项编译这个项目,让它跑快一点。
你可以修改CMakeLists.txt、filter.F90并提交,提交时你可以从五家编译器中选择用你喜爱的一家。
直接默认的文件啥都不动用GCC跑要33s(我用GCC用习惯了),所以先换llvm看看(是的,llvm我没用过),clang要34s……
所以得要对cmake的文件进行优化
cmake_minimum_required(VERSION 3.20)
project(FilterProject LANGUAGES C CXX)
add_executable(program main.cpp filter.F90)
set_source_files_properties(filter.F90 PROPERTIES LANGUAGE C)
target_compile_options(program PRIVATE
-O3 # 启用最高级别优化
-march=native # 针对本地硬件生成优化代码
-ftree-vectorize # 启用自动向量化
-funroll-loops
)上面的优化完跑一下,当时用的是x86-amd,用时5s,很难拿分
借助文心一言(是的,跟gpt斗法一个晚上没斗出结果,跟intel oneapi折腾半天结果是调半天调不明白),然后给我的思路是在gcc就用上avx指令集做simd,(我超这没想出来当时我是不是猪……)
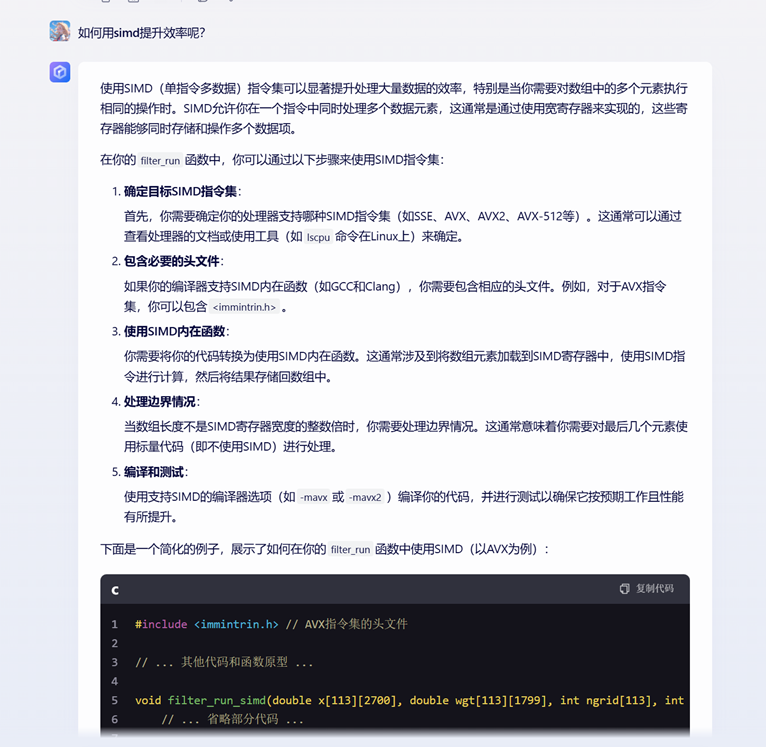
把头文件重新发给gpt,写了一份儿新的filter文件:
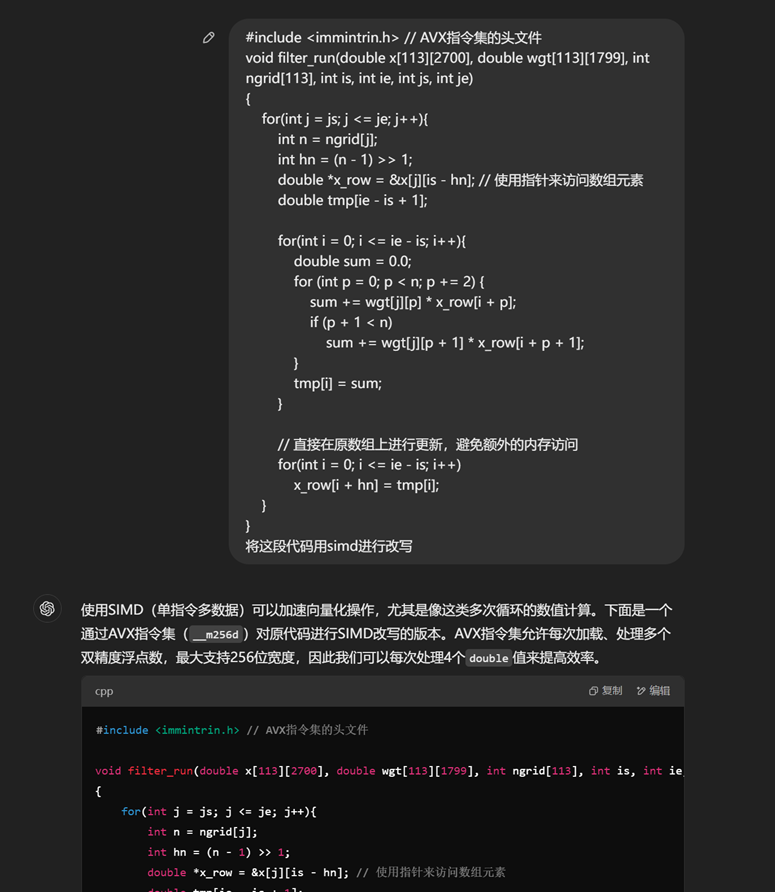
后来搜索引擎再给我一个思路就是内存对齐的效果更好,委托gpt重新写了一版
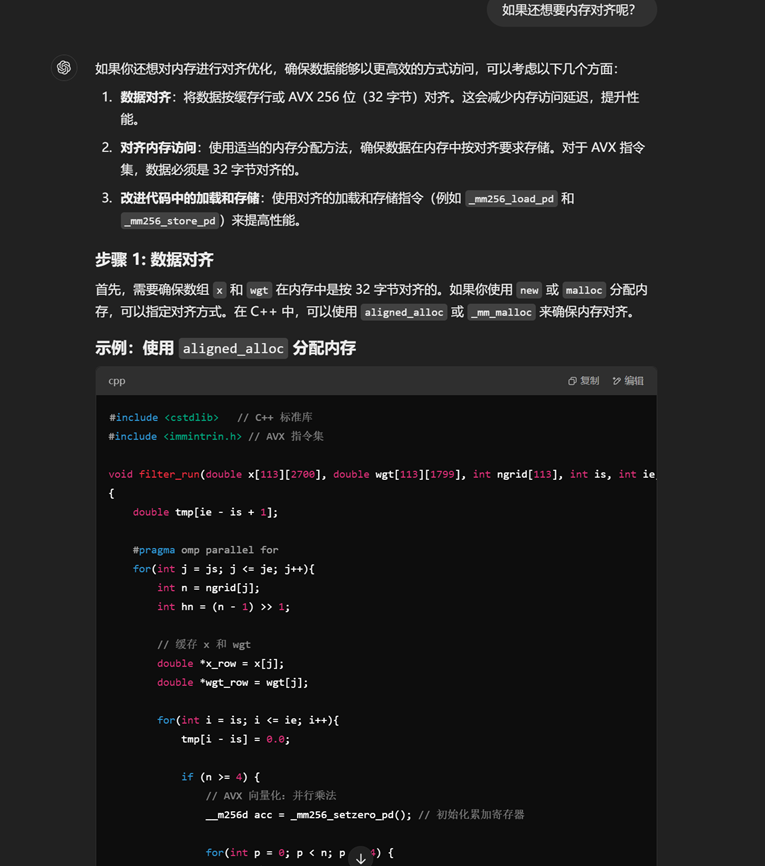
粘贴,make,0.7s
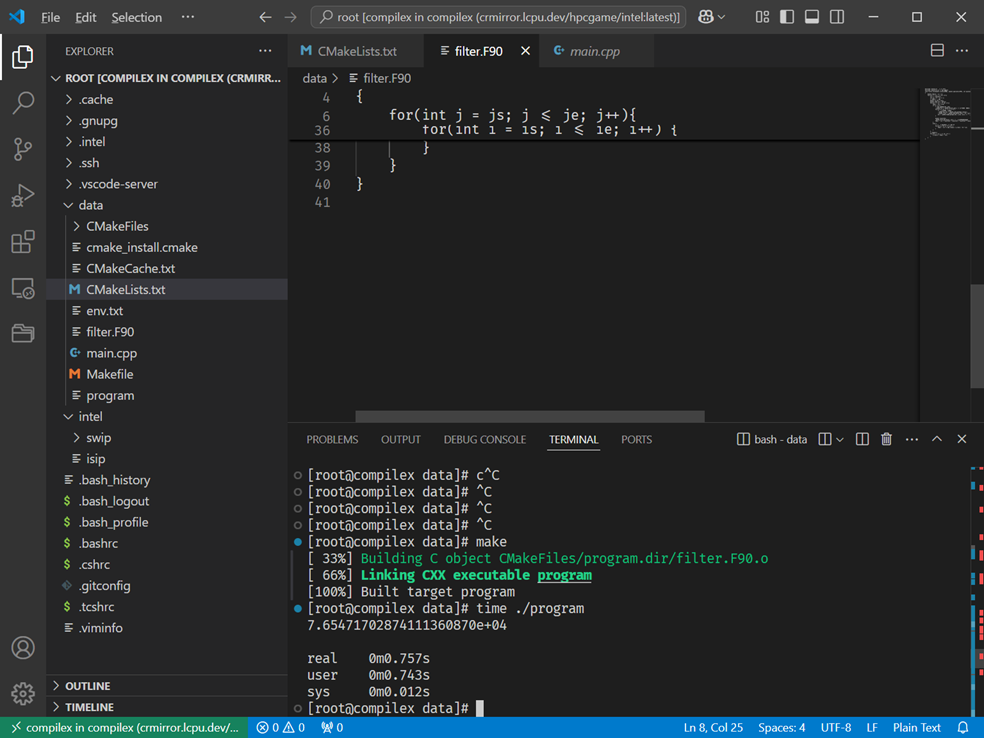
更新:等C题的评测机好了之后,精度过不去
所以filter.f90不动,我就尝试改cmakelist.txt,90分稳定过了……
D题:
说明
给定两个序列,长度分别是len1和len2,输出他们最长公共子序列的长度。
输入输出
输入文件input.dat包含两个序列,格式如下:
首先是两个size_t类型的整数len1和len2,分别表示两个序列的长度。
接下来是两个长度分别为len1和len2的element_t类型的数组,分别表示两个序列。本题中element_t是一个int类型。
输出文件output.dat包含一个size_t类型的整数,表示最长公共子序列的长度。
样例
input.dat
5 6 1 2 3 4 5 1 2 3 4 5 6
output.dat
5
自己改了几个函数结果交上去直接0……提示找不到output.txt
交baseline的试试?喜提7分……
所以又得优化
先开个并行化,然后想起来前几天看的并行计算导论提到按列走效率会高点,所以改了一下:
#include <vector>
#include <utility>
#include <cstdlib>
#include <algorithm>
#include <omp.h>
typedef int element_t;
size_t lcs(element_t* arr_1, element_t* arr_2, size_t len_1, size_t len_2) {
std::vector<size_t> previous(len_2 + 1, 0); // previous row
std::vector<size_t> current(len_2 + 1, 0); // current row
// 对内存访问顺序进行优化,保证数据按列访问
for (size_t i = 1; i <= len_1; ++i) {
#pragma omp parallel for num_threads(16)
for (size_t j = 1; j <= len_2; ++j) {
if (arr_1[i - 1] == arr_2[j - 1]) {
current[j] = previous[j - 1] + 1;
} else {
current[j] = std::max(current[j - 1], previous[j]);
}
}
previous.swap(current); // 交换 current 和 previous
}
return previous[len_2]; // 结果在最后的 previous 行
}交过去19分……
后来gpt就开始掉链子,然后在Pod上都跑错结果,要么就是效率不理想,发了好几次就差一次机会了,我想到这是华为鲲鹏,arm架构,那就利用arm架构的arm neon,gpt助我!
![R7Z(RS]XEKUXHO`39RZ@B@4.png](https://blog.muwinds.com/wp-content/uploads/2025/01/202501261737822210577098.png)
Pod上试了几个数据,我去,这次gpt给力,交了,61分
#include <utility>
#include <cstdlib>
#include <algorithm>
#include <omp.h>
#include <arm_neon.h>
typedef int element_t;
size_t lcs(element_t* arr_1, element_t* arr_2, size_t len_1, size_t len_2) {
size_t* previous = (size_t*)calloc(len_2 + 1, sizeof(size_t));
size_t* current = (size_t*)calloc(len_2 + 1, sizeof(size_t));
for (size_t i = 1; i <= len_1; ++i) {
// Parallelize the inner loop for each row, ensure correct data handling
#pragma omp parallel for
for (size_t j = 1; j <= len_2; j += 4) { // Process 4 elements at a time with NEON
// Load 4 elements from arr_2[j-1..j+3]
int32x4_t arr_2_values = vld1q_s32(&arr_2[j - 1]);
// Process 4 elements of arr_1[i-1]
size_t prev_val = previous[j - 1]; // Initialize with previous[j-1]
int32x4_t current_vals = vld1q_s32(&arr_1[i - 1]);
// Compare 4 elements at once
uint32x4_t match_mask = vceqq_s32(arr_2_values, current_vals);
// Find maximum in current and previous rows, update current
for (size_t k = 0; k < 4 && j + k <= len_2; ++k) {
if (arr_1[i - 1] == arr_2[j + k - 1]) {
current[j + k] = previous[j + k - 1] + 1;
} else {
current[j + k] = std::max(current[j + k - 1], previous[j + k]);
}
}
}
// Ensure all threads are synchronized before swapping
#pragma omp barrier
// Swap current and previous arrays after all threads finish updating
std::swap(current, previous);
}
size_t result = previous[len_2];
free(previous);
free(current);
return result;
}i题:

评测环境是cuda
cuda我很少玩,有个大概的了解
借助gpt……
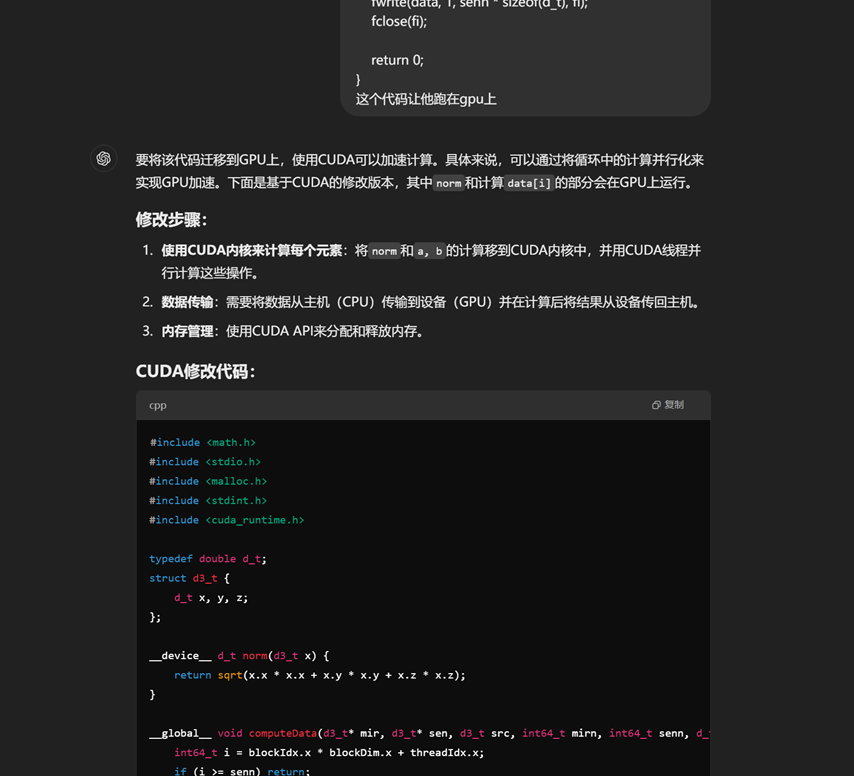
感觉纯cudaMemCpy会出问题,以及这把减法操作给整没了,我自己加上去(再加了个__device__前缀),再让他用cudaMallocManaged改了改,交上去,16分。
接下来开始折腾各种内存优化和对齐,最后尝试预处理,v100的pods上提升不错,交上去一看,从16%涨到26%,血赚
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <vector_types.h>
#include <cuda_runtime.h>
typedef double d_t;
struct d3_t { d_t x, y, z; };
__device__ d3_t operator-(const d3_t& a, const d3_t& b) {
return {a.x - b.x, a.y - b.y, a.z - b.z};
}
__device__ d_t norm(const d3_t& v) {
return sqrt(v.x*v.x + v.y*v.y + v.z*v.z);
}
__constant__ d3_t c_src;
__global__ void computeDist1(const d3_t* __restrict__ mir, d_t* dist1, int64_t mirn) {
int64_t j = blockIdx.x * blockDim.x + threadIdx.x;
if (j >= mirn) return;
dist1[j] = norm(mir[j] - c_src);
}
__global__ void computeData(const d3_t* mir, const d_t* dist1,
const d3_t* sen, int64_t mirn, int64_t senn,
d_t* data, int tile_size) {
extern __shared__ char shared_mem[];
d3_t* shared_mir = (d3_t*)shared_mem;
d_t* shared_dist1 = (d_t*)(shared_mem + tile_size * sizeof(d3_t));
int64_t sen_idx = blockIdx.x * blockDim.x + threadIdx.x;
if (sen_idx >= senn) return;
const d3_t sensor = sen[sen_idx];
const d_t freq_factor = 6.283185307179586 * 2000;
d_t a = 0.0, b = 0.0;
// 分块处理所有mir元素
for (int64_t tile_start = 0; tile_start < mirn; tile_start += tile_size) {
int64_t tile_end = min(tile_start + tile_size, mirn);
int64_t num_in_tile = tile_end - tile_start;
// 协作加载当前tile到共享内存
for (int64_t j = threadIdx.x; j < num_in_tile; j += blockDim.x) {
int64_t global_idx = tile_start + j;
if (global_idx < mirn) {
shared_mir[j] = mir[global_idx];
shared_dist1[j] = dist1[global_idx];
}
}
__syncthreads();
// 处理当前tile中的元素
for (int64_t j = 0; j < num_in_tile; ++j) {
d3_t mirror = shared_mir[j];
d_t dist1_val = shared_dist1[j];
d_t dist2 = norm(mirror - sensor);
d_t phase = freq_factor * (dist1_val + dist2);
d_t cos_val, sin_val;
sincos(phase, &sin_val, &cos_val);
a += cos_val;
b += sin_val;
}
__syncthreads(); // 确保下一tile加载前完成计算
}
data[sen_idx] = hypot(a, b);
}
int main() {
FILE* fi = fopen("in.data", "rb");
d3_t src;
int64_t mirn, senn;
d3_t *mir, *sen;
fread(&src, sizeof(d3_t), 1, fi);
fread(&mirn, sizeof(int64_t), 1, fi);
mir = (d3_t*)malloc(mirn * sizeof(d3_t));
fread(mir, sizeof(d3_t), mirn, fi);
fread(&senn, sizeof(int64_t), 1, fi);
sen = (d3_t*)malloc(senn * sizeof(d3_t));
fread(sen, sizeof(d3_t), senn, fi);
fclose(fi);
// 设备内存分配
d3_t *d_mir, *d_sen;
d_t *d_data, *d_dist1;
cudaMalloc(&d_mir, mirn * sizeof(d3_t));
cudaMalloc(&d_sen, senn * sizeof(d3_t));
cudaMalloc(&d_data, senn * sizeof(d_t));
cudaMalloc(&d_dist1, mirn * sizeof(d_t)); // 预计算dist1的数组
// 将src拷贝到常量内存
cudaMemcpyToSymbol(c_src, &src, sizeof(d3_t));
// 创建多个CUDA流
const int num_streams = 4;
cudaStream_t streams[num_streams];
for (int i = 0; i < num_streams; ++i) {
cudaStreamCreate(&streams[i]);
}
// 同步传输mir数据并预计算dist1
cudaMemcpy(d_mir, mir, mirn * sizeof(d3_t), cudaMemcpyHostToDevice);
dim3 block_pre(512);
dim3 grid_pre((mirn + block_pre.x - 1) / block_pre.x);
computeDist1<<<grid_pre, block_pre>>>(d_mir, d_dist1, mirn);
cudaDeviceSynchronize(); // 确保预计算完成
// 检查共享内存需求
int max_shared_mem_per_block;
cudaDeviceGetAttribute(&max_shared_mem_per_block, cudaDevAttrMaxSharedMemoryPerBlock, 0);
size_t per_element_size = sizeof(d3_t) + sizeof(d_t); // 每个mir元素需要的共享内存
size_t tile_size = max_shared_mem_per_block / per_element_size;
if (tile_size == 0) tile_size = 1; // 确保至少处理一个元素
// 分块处理时使用二维拷贝优化
size_t chunk = (senn + 3) / 4;
for (int i = 0; i < num_streams; ++i) {
cudaStreamCreate(&streams[i]);
size_t offset = i * chunk;
size_t valid = min(chunk, senn - offset);
if (valid == 0) continue;
// 异步拷贝传感器数据
cudaMemcpyAsync(d_sen + offset, sen + offset,
valid * sizeof(d3_t),
cudaMemcpyHostToDevice,
streams[i]);
dim3 block(512);
dim3 grid((valid + block.x - 1) / block.x);
// 计算所需共享内存大小
size_t shared_mem_size = tile_size * (sizeof(d3_t) + sizeof(d_t));
computeData<<<grid, block, shared_mem_size, streams[i]>>>(
d_mir, d_dist1, d_sen + offset,
mirn, valid, d_data + offset, tile_size
);
}
// 同步所有流并销毁
for (int i = 0; i < num_streams; ++i) {
cudaStreamSynchronize(streams[i]);
cudaStreamDestroy(streams[i]);
}
// 拷贝结果回主机
d_t* host_data = (d_t*)malloc(senn * sizeof(d_t));
cudaMemcpy(host_data, d_data, senn * sizeof(d_t), cudaMemcpyDeviceToHost);
// 输出结果
FILE* fo = fopen("out.data", "wb");
fwrite(host_data, sizeof(d_t), senn, fo);
fclose(fo);
// 释放资源
free(mir);
free(sen);
free(host_data);
cudaFree(d_mir);
cudaFree(d_sen);
cudaFree(d_data);
return 0;
}K题:
靓号生成器
Beauty begins with the first hexadecimal digit
题目描述
【提醒:附件 Tab 中有 baseline】
小鸣最近迷上了区块链,他发现每个人的密钥地址是一个以"0x"开头的42位十六进制字符串,例如:
0x7d1a13c226F9951F44392a5446dF518bAE240cFe
作为一个极客,小鸣想要一些特殊的靓号地址。比如他想要一个以"888"开头的密钥地址,那就是类似:
0x888xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
这样的地址。
生成一个密钥n地址的过程是:
- 随机生成一个32字节的私钥
- 用椭圆曲线算法(secp256k1)根据私钥生成公钥
- 取公钥的Keccak-256(SHA3)哈希值的后20字节作为地址
你的任务是帮助小鸣寻找他想要的靓号。
输入格式
从vanity.in,表示想要的地址前缀(不包含"0x"),每行一个,共10个。保证前缀由十六进制字符(0-9,a-f)组成,长度为6。
输出格式
输出到vanity.out,对于vanity.in的每一行输入,输出两行:
- 第一行是找到的完整地址(包含"0x")
- 第二行是对应的私钥的十六进制表示(64位十六进制字符)
样例输入文件
171155 1114a2 12110d 1115c1 141125 111569 111340 11120f 11139a 11112b
样例输出文件
0x17115578a0a064245393165842283c52aecd9c86 c0f41a77bd65228406a0ea94793e4291c839ce0caeb7c6222ca079f70fc2aae6 0x1114a29bbb9df0054ac71c885bbdcd28ae60144d c8e61d9f2e8f7135bef5bc1229911b2f76b5a58ec44ce4ba27802d50b4dd023d 0x12110d4c7375ada8c3136c5cc8aaf0b3f4e81476 c11d97179ec80ab0eee1b554663d4e9ca366c001c15a47d726bde3e3efc403fe 0x1115c119687c793ffb48713f892bec4d4e41ea06 3345a82eda0445269c1f1c58fb9b9f5b9205687227aa4b7b173e485c84fddd75 0x14112520013f9b825baf6a18d926c2a9200a6935 b28f0a7e17a34b05078f54cd92259cb4250c2cce585f5324f56b21e928f73f1f 0x1115694f0b8d1830b7a980919f3e395b20add55d 187cf8b506f2ecde0f4941505f87c0e23dc258d9a8c1b741c17f072fcf3d4dd9 0x1113403525cb1d3779ce3d07324d756a4fcca011 cf36074ed78da76dc346fda35f87a8c88dfd460be3478ee759df805eb3e3daf5 0x11120fcc1d03f7c100a28c2de3f3c4bc54fbe9f2 4437b65386ffb9be43fa344eeab38da7b6513c0d5a06a874860d2f9537d7c3e8 0x11139aeb7403ff90616df43eb619185305b443f5 f2ac2544e46884d6c69433f2de5b174a281c315f107694d9c486ef72ed83995f 0x11112b4798a26153d80cb05e99982049510a7db4 7709e4d5ac06b532f985d4e6ce38eb163ee6c4721f4f32fbcec740467b9495f9
运行环境
容器名为vanity。
附件中有handout,其中包含了baseline、正确性检查工具与secp256k1库。builddeps.sh可以帮你编译依赖库,生成可执行文件vanity、正确性检查工具chk并运行。
评分标准
提交一个vanity.cpp,程序将在 Intel® Xeon® Platinum 8358 Processor 的8个核心上运行。
评测命令行:
g++ -O3 -march=native vanity.cpp -o vanity -lsecp256k1 -lcrypto -fopenmp -lpthread
./vanity运气大师,交baseline居然过了?
![DG5LU]@L[FH8L6Q89Z%6MA8.png](https://blog.muwinds.com/wp-content/uploads/2025/01/202501261737822391780723.png)
但是也用pthread重写了一版就是,交上去报wa,蚌埠
J题:
HPL-MxP
In theory, theory and practice are the same. In practice, they are not.
背景
性能测试一直是 HPC 领域最重要的课题之一。1979年,Jack Dongarra 等人发布了 LINPACK benchmarks,至今仍然是性能测试的事实标准之一。2024年11月的Top500榜单中,El Capitan 以 1,742.00PFlops/s 的成绩位居榜首。这个成绩是通过运行 HPL 测试得到的。
随着时代的发展,fp64 不再是衡量 HPC 系统性能的唯一标准。fp16、int8、int4、int1 等低精度计算也逐渐成为 HPC 领域的热点。同时,为了符合 AI 等负载的需求,硬件制造商也在有意降低硬件的 fp64 性能发展速度,将更多面积用在更低精度的计算上。因此,HPL 也需要不断更新,以适应新的硬件和应用场景。
目标
HPL-MxP 也叫 HPL-AI,旨在使用充分利用 fp16 等精度较低的硬件进行 fp64 计算,提高 HPL 的性能。
任务
本题介绍的是用 32 位浮点数实现的 HPL-MxP,这也是 HPL-MxP 的官方实现。你可以使用任意方法进行加速。
评测
评测容器镜像:hpckit。程序运行在配备 Kunpeng 920 处理器的服务器上,可以使用 2 个核心,10G内存。保证 module 命令可用,没有加载任何模块,请在run.sh中加载自己所需的环境。
为了方便你获取没有加载任何变量的环境,你可以用full容器,我们提供的yaml也是如此。hpckit容器会默认启用bisheng编译器,本题评测时我们进行了特殊处理。
我们会在hpl-mxp 目录中 bash run.sh 来编译并运行你的程序。注意,hpl-ai.c程序不可修改,会以hpc-ai.o的形式提供在程序运行目录,其中包括了 main 函数及其他性能无关函数。你可以参考现有的Makefile使用hpl-ai.o。
bash run.sh
最终得分与对应有效算力成正比。满分为 105 GFLOPs,baseline 为 10 GFLOPs。假设有效算力为xx,你的得分为 x−5x−5 。
提交
请将你的代码打包成 submission.tar 并提交,应该具有如下结构。如果收到“run.sh无法找到”的报错,请注意第一级文件夹的名字应该是hpl-mxp
|-- hpl-mxp # 必须是hpl-mxp |-- hpl-ai.c |-- run.sh |-- Makefile |-- ...
参考
- HPL-MxP
- 华为HPCKit介绍
- Fugaku超算的HPL-MxP实现:解决本题并不需要用到这个仓库,但可以参考它的高性能ARM SVE内核实现
直接跑baseline会过了第一个环节的浮点转换就会卡死,所以跟着主函数文件来到sgetrf那个玩意儿
试过neon的simd啥的,包没用的,很快就能关注到题目中的arm sve,chatgpt继续登场:
![{1D{VZCA0QNME]BOH[JLR9A.png](https://blog.muwinds.com/wp-content/uploads/2025/01/202501261737822441184984.png)
C++
#include <stdio.h>
#include<omp.h>
#include <arm_sve.h>
#include <stddef.h>
#include "hpl-ai.h"
#define A(i, j) *HPLAI_INDEX2D(A, (i), (j), lda)
void sgetrf_nopiv(int m, int n, float *A, int lda) {
int j;
int nb = 32;
int jb = nb;
// Use unblock code.
if (nb > m || nb > n) {
sgetrf2_nopiv(m, n, A, lda);
return;
}
int min_mn = m < n ? m : n;
for (j = 0; j < min_mn; j += nb) {
if (min_mn - j < nb) {
jb = min_mn - j;
}
// Factor panel
sgetrf2_nopiv(m - j, jb, &A[j * lda + j], lda);
if (j + jb < n) {
// strsm optimization with SVE
svbool_t pg = svptrue_b32(); // Create a mask for all elements
svfloat32_t vec_A_jj = svld1_f32(pg, &A[j * lda + j]);
svfloat32_t vec_A_jj_next = svld1_f32(pg, &A[(j + jb) * lda + j]);
// Create a vector with all elements set to 1.0f
svfloat32_t one = svdup_f32(1.0f);
// Perform matrix multiply add (svmla)
svfloat32_t result = svmla_f32_x(pg, vec_A_jj, vec_A_jj_next, one);
svst1_f32(pg, &A[(j + jb) * lda + j], result);
// GEMM with SVE
if (j + jb < m) {
svfloat32_t vec_A_next_row = svld1_f32(pg, &A[(j + jb) * lda + j]);
svfloat32_t vec_A_next_col = svld1_f32(pg, &A[j * lda + j + jb]);
svfloat32_t updated_result = svmul_f32_x(pg, vec_A_next_row, vec_A_next_col);
svst1_f32(pg, &A[(j + jb) * lda + j + jb], updated_result);
}
}
}
}经过9*9=81难的错误调试,总算过了编译顺利跑了起来,然后来到最后的gmres是直接报nan……
G题(julia题):
通知
如果你需要装包,可以这样做:
import Pkg
Pkg.activate(temp=true)
Pkg.add("包")背景
【提醒:附件 Tab 中有数据生成器与主程序 】
小 T 最近在学习并行计算,他发现在大规模数据处理中,寻找最大的 K 个元素是一个非常常见的需求。比如在搜索引擎中,需要找出最相关的前 K 个结果;在推荐系统中,需要推荐最匹配的 K 个商品。
小 T 想要实现一个高效的 Top-K 算法,他希望你能帮助他完成这个任务。而 Julia 最近在科学计算领域,因其方便的并行计算和高性能的特性,受到了越来越多的关注。所以小 T 希望你使用 Julia 语言来实现这个算法,并尽可能地优化其性能。
说明
给定一个包含 N 个数(整数或浮点数)的数组,找出其中最大的 K 个数。
你需要实现一个签名为 topk(data, k) 的函数,其中 data 是一个包含 N 个数(整数或浮点数)的数组,k 是一个正整数。
函数的返回值是一个包含 K 个整数的数组,这 K 个数是输入数组中最大的 K 个数的下标(从 1 开始),且应当按照下标对应数值从大到小排序。如果输入数组中存在多个相同的数,则下标小的优先。
你不需要考虑文件输入或输出,只需要实现 topk 函数。评测程序将会调用你的实现进行评测。
评测环境
容器镜像:julia。已设置环境变量 JULIA_PKG_SERVER,无需担心装包的网络问题。
运行选手程序前,会先运行 julia -e 'using Pkg; Pkg.instantiate()' 来安装依赖。
评测方法
提交一个 impl.jl 文件,包括 topk函数,函数签名是:
@inbounds function topk(data::AbstractVector{T}, k) where T
# your code here
end评测时使用 Julia 1.11.2 版本。
程序会在配备 Intel® Xeon® Platinum 8358 Processor 的服务器上以 julia -t 8 的方式运行,也即可以使用 8 个线程。
评分标准
所有结果必须正确,否则不得分。
测试点如下所示,其中 N 是数组长度,K 是需要找的最大数的个数,N 和 K 都为 2 的幂。每道题中整型(Int64)与浮点型(Float64)测试点分开计算,占比均为50%。
- N = 8192,K = 8 :10 分,结果正确即可得分,运行时间需小于 1 分钟。
- N = 32768, K = 128:20分,结果正确即可得分,运行时间需小于 1 分钟。
- N = 220220, K = 256:40分,按性能赋分。
- N = 230230, K = 1024:130分,按性能赋分。
对于按性能赋分的测试点,对比你的实现与标准库中单线程的实现,计算加速比为 x,得分计算方法如下。其中 f(x)f(x) 为 sigmoid 函数变体。
| 得分 | 整形加速比 | 浮点加速比 |
|---|---|---|
| 0% | x < 2 | x < 2 |
| f(x)f(x) | x | x |
| 100% | x >= 10 | x >= 13 |
我们给出评测用的baseline用时和std运行时间如下:
- N = 8192, baseline: 0.238063315, 0.246213896, std: 0.000169, 0.000112
- N = 32768, 0.000344826, 0.000510477, std: 0.000118, 0.000142
- N = 220220, 0.006957641, 0.014872915, std: 0.000611, 0.000951
- N = 230230, 9.672722409, 18.007807025, std: 0.470093, 0.769184
提示
- Julia 标准库中的
partialsort和partialsortperm函数可以实现 Top-K 的计算。 - 关于 Julia 性能优化,可以参考官网的 Performance Tips。
- 可能会有帮助的一些第三方 Julia 库:
- BenchmarkTools
- JET
- PProf
- 陈久宁老师的Julia讲座对新手很友好。Julia 教程可以参考 官方文档。中文材料可以参考李东风老师的 Julia 语言入门。我们的 Julia沙龙介绍了一些 Julia 可能出现性能问题的原因。
- TopK 算法的一种实现思路是使用基数排序,可以参考这篇文章。
impl.jl中也有一些提示,可以参考。
开始先简单用std糊弄了个:
using Base.Threads
# 原子类型定义,用于线程安全的操作
mutable struct Atomic{T}; @atomic x::T; end
@inbounds function topk(data::AbstractVector{T}, k) where T
# 将数值和下标配对
indexed_data = [(i, data[i]) for i in 1:length(data)]
# 数据划分为8份
num_threads = nthreads()
chunk_size = div(length(data), num_threads)
chunks = [indexed_data[(i-1)*chunk_size+1:min(i*chunk_size, length(data))] for i in 1:num_threads]
# 定义一个并行函数,处理每个线程的排序和选择最大K个
function parallel_sort(chunk)
return sort(chunk, by = x -> (-x[2], x[1]))[1:k]
end
# 创建一个数组来存储每个线程的局部结果
results = Vector{Tuple{Int, T}}(undef, k * num_threads)
# 使用多个线程并行化排序操作
@threads for i in 1:num_threads
local_sorted = parallel_sort(chunks[i])
# 将结果写入共享数组
for j in 1:k
results[(i-1)*k + j] = local_sorted[j]
end
end
# 合并所有线程的结果并进行排序
final_sorted = sort(results, by = x -> (-x[2], x[1]))
# 返回前K个下标
return [final_sorted[i][1] for i in 1:k]
end30分骗到手
但是后面的难如登天,借助文心一言改写成堆排序自己再改simd和inbounds也就32分……
import Pkg
Pkg.activate(temp=true)
Pkg.add("DataStructures")
using Base.Threads
using DataStructures
# 并行化选择TopK的下标的核心计算函数
function parallel_topk_indices(chunk::Vector{Tuple{Int, T}}, k::Int) where T
# 使用最大堆来选择TopK的下标
max_heap = BinaryMaxHeap{Tuple{T, Int}}()
for (idx, value) in chunk
# 插入堆中,堆按值的大小自动排序(这里是负值因为BinaryMaxHeap是最大堆)
push!(max_heap, (-value, idx)) # 负值以模拟最大堆行为
# 如果堆的大小超过k,移除最小的元素
if length(max_heap) > k
pop!(max_heap)
end
end
# 从堆中提取元素,并获取下标
result = Vector{Int}(undef, length(max_heap))
@simd for i in 1:length(max_heap)
(_, idx) = pop!(max_heap)
result[i] = idx
end
return result
end
# 主函数:计算前K大的数的下标
@inbounds function topk(data::Vector{T}, k::Int) where T
# 数据划分为线程数份
num_threads = nthreads()
chunk_size = div(length(data), num_threads)
# 预分配存储结果的数组
results = Vector{Int}(undef, k * num_threads)
all_indices = Vector{Int}(undef, k * num_threads) # 确保大小足够大
# 使用多个线程并行化排序操作
@threads for i in 1:num_threads
# 计算每个线程的分片范围
start_idx = (i - 1) * chunk_size + 1
end_idx = min(i * chunk_size, length(data))
# 提取当前分片的数据
local_chunk = [(idx, data[idx]) for idx in start_idx:end_idx]
# 对当前分片进行TopK下标选择
local_topk_indices = parallel_topk_indices(local_chunk, k)
# 将结果写入共享数组(按线程对应位置)
offset = (i - 1) * k
for j in 1:k
results[offset + j] = local_topk_indices[j]
end
end
# 合并所有线程的结果
# 只合并有效的K个元素,避免超出数组边界
all_indices[1:k*num_threads] .= results[1:k*num_threads]
# 使用这些下标从原始数据中获取对应的值
values = data[all_indices]
# 对值进行排序,并选择前K个元素对应的下标
sort_perm = sortperm(values, rev=true)
final_topk_indices = all_indices[sort_perm[1:k]]
return final_topk_indices
end最后靠deepseek躺赢的一局
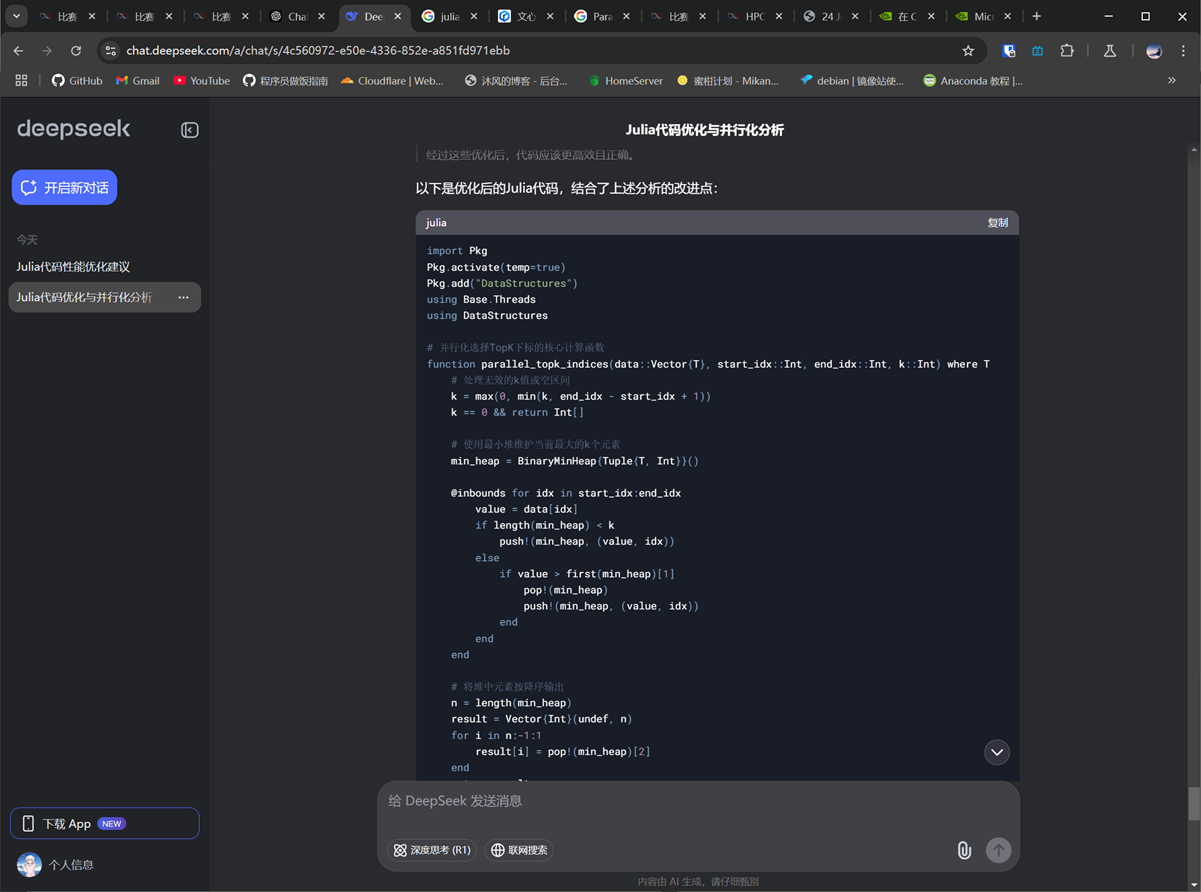
import Pkg
Pkg.activate(temp=true)
Pkg.add("DataStructures")
using Base.Threads
using DataStructures
# 并行化选择TopK下标的核心计算函数
function parallel_topk_indices(data::Vector{T}, start_idx::Int, end_idx::Int, k::Int) where T
# 处理无效的k值或空区间
k = max(0, min(k, end_idx - start_idx + 1))
k == 0 && return Int[]
# 使用最小堆维护当前最大的k个元素
min_heap = BinaryMinHeap{Tuple{T, Int}}()
@inbounds for idx in start_idx:end_idx
value = data[idx]
if length(min_heap) < k
push!(min_heap, (value, idx))
else
if value > first(min_heap)[1]
pop!(min_heap)
push!(min_heap, (value, idx))
end
end
end
# 将堆中元素按降序输出
n = length(min_heap)
result = Vector{Int}(undef, n)
for i in n:-1:1
result[i] = pop!(min_heap)[2]
end
return result
end
# 主函数:计算前K大的数的下标
@inbounds function topk(data::Vector{T}, k::Int) where T
len = length(data)
k = min(k, len)
len == 0 && return Int[]
num_threads = nthreads()
chunk_size = div(len, num_threads)
# 存储各线程结果的数组
thread_results = Vector{Vector{Int}}(undef, num_threads)
@threads for i in 1:num_threads
start_idx = (i-1)*chunk_size + 1
end_idx = i == num_threads ? len : i * chunk_size
# 直接处理数据分片,避免创建临时数组
thread_results[i] = parallel_topk_indices(data, start_idx, end_idx, k)
end
# 合并所有结果
all_indices = vcat(thread_results...)
# 当总候选数不超过k时直接返回
length(all_indices) <= k && return all_indices
# 高效部分排序获取前k大元素的下标
values = data[all_indices]
sort_order = partialsortperm(values, 1:k, rev=true)
return all_indices[sort_order]
endE题:
更新
目前版本的评测机可用如下的代码输出到文件,文件末尾不应有额外换行。请实现从命令行参数读取输入文件位置的功能,不要硬编码forest.in。
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
fo << grid[i * n + j] << " ";
}
fo << std::endl;
}本题评测机的运行脚本,供参考:
. /etc/profile >/dev/null #加载环境krun init >/dev/nullif [ "$JOB_COMPLETION_INDEX" -eq 0 ]; then
krun host -n -H > hostfile
mpirun --hostfile hostfile -np 64 -ppn 16 /data/forest /problem/input.dat /data/output.datelse
sleep infinityfi因为选手的pod本来就是sleep infinity开启的,所以你可以登录任意的pod,运行:
. /etc/profile >/dev/null #加载环境krun init >/dev/null
krun host -n -H > hostfile
mpirun --hostfile hostfile -np 4 -ppn 1 /data/forest /problem/input.dat /data/output.dat背景描述
在西西努努魔法大陆的一片神秘的森林中,生长着一种神奇的树木——呆呆树。呆呆树不仅外表呆萌,还有一个奇特的性质:它们虽然会燃烧,但永远不会完全消失!当火灾发生时,呆呆树会从树木状态转化为燃烧状态,最终变成灰烬。然而,灰烬中蕴藏着生机,在魔法的作用下,呆呆树就能从灰烬中重生!
近日,这片森林并不太平,一场火灾打破了森林的宁静。在火灾蔓延的同时,黑魔法师乌乌和善良的魔法师芙芙正在这片森林中展开一场激烈的对抗。乌乌可以使用魔法召唤惊雷,点燃森林中的某棵呆呆树,试图用火焰吞噬一切。而芙芙则不甘示弱,她可以用神奇的魔法妙手回春,让一定区域内的呆呆树灰烬重新焕发生机,从而拯救这片森林。两人的魔法在森林中交织,火势时而蔓延,时而消退,呆呆树的状态也在不断变化。
作为森林的守护者,你需要模拟火灾的蔓延过程,从而获知呆呆树的状态变化。由于森林的面积很大,为了加快模拟的速度,你想到了借助 MPI 的力量,将模拟任务分配到多个进程中并行处理。时间紧迫,快来帮助人们拯救这片森林吧!
任务描述
你需要模拟一个 n×nn×n 的呆呆树森林网格,森林网格的坐标范围为 [0,n−1]×[0,n−1][0,n−1]×[0,n−1] 。每个格点可能是以下四种状态之一:
- 0:空地
- 1:树木
- 2:燃烧
- 3:灰烬
呆呆树的状态会随着时间的变化而更新。模拟以时间步为粒度进行,每个时间步分为两个阶段:
- 魔法事件阶段:
- 天降惊雷:黑魔法师乌乌在坐标 (x,y)(x,y) 处落下惊雷。如果坐标 (x,y)(x,y) 的格点状态为树木(状态1)的话,则将其状态转化为燃烧(状态2)。
- 妙手回春:魔法师芙芙让一片矩形区域 [sx,ex]×[sy,ey][sx,ex]×[sy,ey] 内的灰烬恢复生机。对于矩形区域 [sx,ex]×[sy,ey][sx,ex]×[sy,ey] 内(包含边界)的每一个格点,如果其状态为灰烬(状态3)的话,则将其状态转化为树木(状态1)。
- 在该阶段,可能会发生两种魔法事件:
- 如果该时间步没有魔法事件,则在魔法事件阶段中,森林的状态不会发生任何改变。
- 状态转移阶段:
- 如果一个格点的状态是树木(状态1),且其周围(即上下左右的四个格点)中至少有一个格点的状态是燃烧(状态2),则该格点的状态会转化为燃烧(状态2)。
- 如果一个格点的状态是燃烧(状态2),则该格点的状态会转化为灰烬(状态3)。
- 在该阶段,按照以下规则进行状态转移:
在同一时间步中,魔法事件阶段先发生,状态转移阶段后发生。也就是说,在同一时间步中,状态转移阶段的状态输入即为魔法事件阶段的状态输出。
你的任务是模拟火灾的蔓延过程,并输出最终每个格点的状态。
评测环境
容器镜像:intel。编译器已经配置为 mpiicpx,并且已经加载了 mpi 模块。
输入输出约定
输入格式
本题需要从文件读取输入。输入文件为文本文件,,文件名从命令行参数获取。
输入文件的格式如下:
第一行包含三个整数 n ,m 和 t,分别表示网格的边长、魔法事件的数量、模拟的总时间步数。
接下来 n 行,每行包括 n 个整数,表示初始时刻每个格点的状态(0:空地、1:树木、2:燃烧、3:灰烬)。
接下来 m 行,每行描述一个魔法事件,格式为 “<时间步> <事件类型> <参数>”,事件类型包括:
- 1:天降惊雷,参数为惊雷降落处的坐标 x 和 y 。题目输入保证 0≤x,y≤n−10≤x,y≤n−1 。
- 2:妙手回春,参数为矩形区域的范围 sx,sy,ex,ey 。题目输入保证 0≤sx≤ex≤n−10≤sx≤ex≤n−1 且 0≤sy≤ey≤n−10≤sy≤ey≤n−1 。
在输入文件中,魔法事件的顺序按照其发生的时间步顺序升序排列。并且,每个时间步最多发生一个魔法事件。
你可以使用handout中的gencase.py生成测试数据。
输出格式
你需要把结果输出到输出文件中,文件名从命令行参数获取。
输出的格式为:输出 nn 行,每行包含 nn 个用空格分开的整数,表示最终时刻每个格点的状态。
样例输入输出
样例一
- 输入文件 :
6 2 4 1 1 1 2 1 1 1 0 1 1 1 1 0 1 2 1 0 1 0 1 0 1 0 1 1 1 1 1 1 1 1 0 0 1 0 0 3 2 0 1 2 3 4 1 4 5
- 输出文件:
3 3 3 2 3 3 2 0 2 3 3 3 0 3 2 3 0 2 0 3 0 3 0 2 2 3 2 3 2 3 1 0 0 2 0 0
- 对样例的解释:
本样例的地图尺寸为 6×66×6 ,发生了 22 个魔法事件(分别在时间步 33 和时间步 44 发生),要求输出模拟 44 个时间步之后的模拟结果。
森林的初始状态如下:
1 1 1 2 1 1 1 0 1 1 1 1 0 1 2 1 0 1 0 1 0 1 0 1 1 1 1 1 1 1 1 0 0 1 0 0
时间步 11 没有发生魔法事件,故只进行状态转移。时间步 11 结束后的森林状态如下:
1 1 2 3 2 1 1 0 2 2 1 1 0 2 3 2 0 1 0 1 0 1 0 1 1 1 1 1 1 1 1 0 0 1 0 0
时间步 22 没有发生魔法事件,故只进行状态转移。时间步 22 结束后的森林状态如下:
1 2 3 3 3 2 1 0 3 3 2 1 0 3 3 3 0 1 0 2 0 2 0 1 1 1 1 1 1 1 1 0 0 1 0 0
时间步 33 发生了类型为 22 的魔法事件(即“妙手回春”),范围为 [0,2]×[1,3][0,2]×[1,3] ,该范围内状态3的格点均转化为状态1。时间步 33 的魔法事件阶段结束后,森林状态如下:
1 2 1 1 3 2 1 0 1 1 2 1 0 1 1 1 0 1 0 2 0 2 0 1 1 1 1 1 1 1 1 0 0 1 0 0
紧接着还需要发生时间步 33 的状态转移阶段。时间步 33 结束后的森林状态如下:
2 3 2 1 3 3 1 0 1 2 3 2 0 2 1 2 0 1 0 3 0 3 0 1 1 2 1 2 1 1 1 0 0 1 0 0
时间步 44 发生了类型为 11 的魔法事件(即“天降惊雷”),坐标为 (4,5)(4,5) ,该点的状态恰好为树木(状态1),所以会转变为燃烧(状态2)。时间步 44 的魔法事件阶段结束后,森林状态如下:
2 3 2 1 3 3 1 0 1 2 3 2 0 2 1 2 0 1 0 3 0 3 0 1 1 2 1 2 1 2 1 0 0 1 0 0
紧接着还需要发生时间步 44 的状态转移阶段。时间步 44 结束后的森林状态如下:
3 3 3 2 3 3 2 0 2 3 3 3 0 3 2 3 0 2 0 3 0 3 0 2 2 3 2 3 2 3 1 0 0 2 0 0
即为题目要求输出的状态。
样例二
- 输入文件
forest.in:16 5 7 2 2 1 1 0 2 1 1 1 1 1 1 0 0 1 1 1 0 1 1 1 0 1 0 1 1 1 0 1 1 1 1 0 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 0 1 1 1 2 1 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 0 1 1 1 1 1 0 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 0 1 1 0 1 0 0 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 2 1 1 1 1 1 1 0 0 1 0 1 1 1 1 1 0 0 1 1 1 1 1 0 1 1 0 1 1 1 1 2 4 0 13 2 2 1 7 9 4 2 6 2 12 13 5 2 1 8 13 11 7 1 7 0 - 输出文件
forest.out:3 3 3 3 0 3 3 3 3 3 3 3 0 0 3 3 3 0 3 3 3 0 3 0 3 3 3 0 3 3 3 3 0 3 3 3 3 0 3 3 3 0 3 3 3 3 3 3 3 3 0 3 3 3 3 0 3 0 3 3 3 3 3 0 2 3 2 3 2 3 3 3 0 0 0 3 3 3 0 1 1 2 1 2 0 0 3 3 3 3 3 3 3 0 2 1 2 1 1 1 2 3 3 3 3 3 3 3 3 3 3 2 3 2 1 0 3 3 3 3 3 3 3 0 3 3 2 0 2 1 1 1 2 3 3 0 3 3 3 3 0 2 1 0 2 0 0 1 2 2 0 3 3 3 3 3 3 2 1 1 3 3 3 0 3 2 2 3 3 0 3 3 2 1 1 1 3 3 3 3 3 0 2 2 3 2 0 2 1 1 1 1 3 3 0 3 3 3 3 2 0 1 1 1 1 1 1 1 3 3 3 3 3 3 3 3 2 1 1 1 1 1 1 1 3 0 3 3 3 3 3 3 3 0 0 1 0 1 1 1 3 3 0 0 3 3 3 3 2 0 1 1 0 1 1 1
评分标准
测试环境
本题的评测环境为:4 节点,每节点 16 个核。运行在配备 Intel® Xeon® Platinum 8358 Processor 的服务器上。每个节点配备 32GiB 内存。
测试点和评分标准
本题有一个测试点,规模和评分标准如下。在限制时间内得到正确结果可以得到基本分,在满分时间内得到正确结果可以得到满分,分数随时间线性变化。
| 序号 | n | t | 时间限制 | 满分时间 | 基本分值 | 满分分值 |
|---|---|---|---|---|---|---|
| 1 | 16384 | 2000 | 110s | 68s | 50 | 150 |
纯纯整理好题面给deepseek了,真牛啊,gpt o1折腾半天跟他扯mpi全过程无限删对话开对话,deepseek这个直接出正确答案……
#include <mpi.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#include <unordered_map>
struct Event {
int step;
int type;
int params[4];
};
int main(int argc, char** argv) {
MPI_Init(&argc, &argv);
int rank, size;
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Comm_size(MPI_COMM_WORLD, &size);
int n, m, t;
std::unordered_map<int, Event> events;
int* global_grid = nullptr;
int* event_data = nullptr;
if (rank == 0) {
FILE* fin = fopen(argv[1], "r");
fscanf(fin, "%d %d %d", &n, &m, &t);
global_grid = new int[n * n];
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
fscanf(fin, "%d", &global_grid[i * n + j]);
}
}
events.reserve(m);
for (int k = 0; k < m; ++k) {
Event e;
fscanf(fin, "%d %d", &e.step, &e.type);
if (e.type == 1) {
fscanf(fin, "%d %d", &e.params[0], &e.params[1]);
e.params[2] = e.params[3] = 0;
} else {
fscanf(fin, "%d %d %d %d", &e.params[0], &e.params[1], &e.params[2], &e.params[3]);
}
events[e.step] = e;
}
fclose(fin);
event_data = new int[m * 6];
int idx = 0;
for (const auto& pair : events) {
const Event& e = pair.second;
event_data[idx++] = e.step;
event_data[idx++] = e.type;
event_data[idx++] = e.params[0];
event_data[idx++] = e.params[1];
event_data[idx++] = e.params[2];
event_data[idx++] = e.params[3];
}
}
MPI_Bcast(&n, 1, MPI_INT, 0, MPI_COMM_WORLD);
MPI_Bcast(&m, 1, MPI_INT, 0, MPI_COMM_WORLD);
MPI_Bcast(&t, 1, MPI_INT, 0, MPI_COMM_WORLD);
if (rank != 0) {
event_data = new int[m * 6];
}
MPI_Bcast(event_data, m * 6, MPI_INT, 0, MPI_COMM_WORLD);
if (rank != 0) {
for (int i = 0; i < m; ++i) {
Event e;
e.step = event_data[i * 6];
e.type = event_data[i * 6 + 1];
e.params[0] = event_data[i * 6 + 2];
e.params[1] = event_data[i * 6 + 3];
e.params[2] = event_data[i * 6 + 4];
e.params[3] = event_data[i * 6 + 5];
events[e.step] = e;
}
delete[] event_data;
} else {
delete[] event_data;
}
int remainder = n % size;
int local_rows = n / size + (rank < remainder ? 1 : 0);
int start_row = (rank < remainder) ? (rank * (n / size + 1)) : (remainder * (n / size + 1) + (rank - remainder) * (n / size));
int end_row = start_row + local_rows - 1;
int* local_data = new int[local_rows * n];
if (rank == 0) {
int* ptr = global_grid;
for (int dest = 0; dest < size; ++dest) {
int dest_remainder = n % size;
int dest_local_rows = n / size + (dest < dest_remainder ? 1 : 0);
int dest_start_row = (dest < dest_remainder) ? (dest * (n / size + 1)) : (dest_remainder * (n / size + 1) + (dest - dest_remainder) * (n / size));
if (dest == 0) {
memcpy(local_data, ptr, dest_local_rows * n * sizeof(int));
} else {
MPI_Send(ptr, dest_local_rows * n, MPI_INT, dest, 0, MPI_COMM_WORLD);
}
ptr += dest_local_rows * n;
}
delete[] global_grid;
} else {
MPI_Recv(local_data, local_rows * n, MPI_INT, 0, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
int** current = new int*[local_rows + 2];
int** next = new int*[local_rows + 2];
for (int i = 0; i < local_rows + 2; ++i) {
current[i] = new int[n];
next[i] = new int[n];
if (i >= 1 && i <= local_rows) {
memcpy(current[i], local_data + (i - 1) * n, n * sizeof(int));
} else {
memset(current[i], 0, n * sizeof(int));
}
}
delete[] local_data;
for (int step = 1; step <= t; ++step) {
auto it = events.find(step);
if (it != events.end()) {
const Event& e = it->second;
if (e.type == 1) {
int x = e.params[0];
int y = e.params[1];
if (x >= start_row && x <= end_row) {
int local_x = x - start_row + 1;
if (current[local_x][y] == 1) {
current[local_x][y] = 2;
}
}
} else {
int sx = e.params[0];
int sy = e.params[1];
int ex = e.params[2];
int ey = e.params[3];
int overlap_sx = std::max(sx, start_row);
int overlap_ex = std::min(ex, end_row);
int overlap_sy = std::max(sy, 0);
int overlap_ey = std::min(ey, n - 1);
if (overlap_sx <= overlap_ex && overlap_sy <= overlap_ey) {
for (int x = overlap_sx; x <= overlap_ex; ++x) {
int local_x = x - start_row + 1;
for (int y = overlap_sy; y <= overlap_ey; ++y) {
if (current[local_x][y] == 3) {
current[local_x][y] = 1;
}
}
}
}
}
}
if (rank > 0) {
MPI_Sendrecv(current[1], n, MPI_INT, rank - 1, 0,
current[0], n, MPI_INT, rank - 1, 0,
MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
if (rank < size - 1) {
MPI_Sendrecv(current[local_rows], n, MPI_INT, rank + 1, 0,
current[local_rows + 1], n, MPI_INT, rank + 1, 0,
MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
for (int i = 1; i <= local_rows; ++i) {
for (int j = 0; j < n; ++j) {
int old_val = current[i][j];
if (old_val == 2) {
next[i][j] = 3;
} else if (old_val == 1) {
int up = (i - 1 >= 0) ? current[i - 1][j] : 0;
int down = (i + 1 < local_rows + 2) ? current[i + 1][j] : 0;
int left = (j > 0) ? current[i][j - 1] : 0;
int right = (j < n - 1) ? current[i][j + 1] : 0;
next[i][j] = (up == 2 || down == 2 || left == 2 || right == 2) ? 2 : 1;
} else {
next[i][j] = old_val;
}
}
}
memcpy(next[0], current[0], n * sizeof(int));
memcpy(next[local_rows + 1], current[local_rows + 1], n * sizeof(int));
std::swap(current, next);
}
int* sendbuf = new int[local_rows * n];
for (int i = 0; i < local_rows; ++i) {
memcpy(sendbuf + i * n, current[i + 1], n * sizeof(int));
}
if (rank == 0) {
int** final_grid = new int*[n];
for (int i = 0; i < n; ++i) {
final_grid[i] = new int[n];
}
for (int i = 0; i < local_rows; ++i) {
memcpy(final_grid[start_row + i], sendbuf + i * n, n * sizeof(int));
}
delete[] sendbuf;
for (int src = 1; src < size; ++src) {
int src_remainder = n % size;
int src_local_rows = n / size + (src < src_remainder ? 1 : 0);
int* recvbuf = new int[src_local_rows * n];
MPI_Recv(recvbuf, src_local_rows * n, MPI_INT, src, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
int src_start_row = (src < src_remainder) ? (src * (n / size + 1)) : (src_remainder * (n / size + 1) + (src - src_remainder) * (n / size));
for (int i = 0; i < src_local_rows; ++i) {
memcpy(final_grid[src_start_row + i], recvbuf + i * n, n * sizeof(int));
}
delete[] recvbuf;
}
FILE* fout = fopen(argv[2], "w");
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (j != 0) fprintf(fout, " ");
fprintf(fout, "%d", final_grid[i][j]);
}
fprintf(fout, "\n");
}
fclose(fout);
for (int i = 0; i < n; ++i) {
delete[] final_grid[i];
}
delete[] final_grid;
} else {
MPI_Send(sendbuf, local_rows * n, MPI_INT, 0, 0, MPI_COMM_WORLD);
delete[] sendbuf;
}
for (int i = 0; i < local_rows + 2; ++i) {
delete[] current[i];
delete[] next[i];
}
delete[] current;
delete[] next;
MPI_Finalize();
return 0;
}不过这个题倒是让我折腾半天mpi相关的部署和运行……
L题:
Accelerating EDA
注:更新了 Baseline。Input 位于只读文件系统,所以需要以只读方式打开;请修改您的代码,以避免出现 Assertion Error。
背景
EDA,也就是电子设计自动化,是一种用于设计电子系统的方法。EDA工具可以帮助工程师设计和分析电子系统,从而提高设计效率。EDA工具通常包括模拟仿真、数字仿真、布局设计、布线设计等功能,帮助工程师快速设计出高质量的电子系统。正是 EDA,使大规模集成电路的设计成为可能,推动了电子系统的发展。
EDA的主要任务包括:
- 逻辑设计:使用硬件描述语言(如Verilog或VHDL)描述电路的功能。
- 仿真与验证:通过仿真工具验证设计的正确性,确保电路在逻辑和时序上符合预期。
- 综合:将高级的逻辑描述转换为门级网表(gate-level netlist),即由基本逻辑门(如AND、OR、NOT等)组成的电路。
- 布局布线(Place and Route):将逻辑门映射到物理芯片上,并确定它们的位置和连接方式。
- 时序分析:确保电路在物理实现后能够满足时序要求,避免信号延迟等问题。
在EDA的布局布线阶段,布线优化是一个关键问题。布线优化的目标是在满足电路性能要求的前提下,最小化导线的长度和面积,从而减少功耗、提高芯片的性能和可靠性。
随着技术的进展,EDA工具也遇到了很多瓶颈。如布局设计、布线设计等,都是NP完全问题,难以在合理的时间内找到最优解。因此,如何加速EDA工具成为了一个重要的问题。
说明
RSMT
在布线优化中,直角斯坦纳最小树(Rectilinear Steiner Minimal Tree, RSMT)问题是一个经典问题。RSMT的目标是在平面上用直角线(即水平和垂直线)连接一组给定的点(称为引脚或节点),并且可以通过引入额外的点(称为斯坦纳点)来减少总布线长度。RSMT问题的解是一个树结构,称为直角斯坦纳树,它连接了所有的引脚,并且总长度最小。
RSMT问题在VLSI(超大规模集成电路)设计中非常重要,因为它可以用于估计电路的布线长度、布线拥塞和互连延迟。RSMT问题的难点在于它是一个NP完全问题,意味着随着引脚数量的增加,问题的复杂度会急剧上升,难以在多项式时间内找到最优解。
FLUTE 方法
FLUTE(Fast Lookup Table Based Rectilinear Steiner Minimal Tree Algorithm)是一种基于查找表的快速RSMT算法,专门用于VLSI设计中的低度网络(即引脚数量较少的网络)。FLUTE的核心思想是通过预计算的查找表来快速构建RSMT,从而在保证高精度的同时,显著提高计算速度。
FLUTE的主要特点:
查找表(Lookup Table):FLUTE通过预计算所有可能的低度网络的RSMT解,并将这些解存储在查找表中。对于给定的网络,FLUTE只需查找表中的相应条目,即可快速得到最优解。
低度网络的优化:FLUTE特别适用于低度网络(引脚数量较少的网络),因为低度网络的解空间较小,查找表可以覆盖所有可能的解。对于高度网络(引脚数量较多的网络),FLUTE使用网络分割技术将网络分解为多个低度子网络,然后分别求解。
精度与速度的权衡:FLUTE允许用户通过调整参数来控制精度和计算速度之间的权衡。用户可以选择更高的精度,但计算时间会相应增加;或者选择更快的计算速度,但精度可能会有所降低。
FLUTE的工作流程:
- 查找表生成:FLUTE首先为低度网络生成查找表。查找表中存储了每个网络的潜在最优布线长度向量(POWV)和对应的潜在最优斯坦纳树(POST)。这些数据是通过边界压缩技术和递归算法生成的。
- 网络分割:对于高度网络,FLUTE使用网络分割技术将网络分解为多个低度子网络。分割时,FLUTE会评估不同的分割方式,并选择最优的分割方案。
- 查找表查询:对于每个低度子网络,FLUTE通过查找表快速找到最优的RSMT解。
- 结果合并:将各个子网络的解合并,得到整个网络的RSMT。
FLUTE的优势:
- 速度快:FLUTE的计算速度非常快,尤其是对于低度网络,几乎可以与RMST(上文是RSMT,这里是RMST,并不相同)算法相媲美。
- 精度高:FLUTE在低度网络上能够找到最优解,对于高度网络也能提供非常接近最优的解。
- 灵活性:FLUTE允许用户通过调整参数来控制精度和计算速度之间的权衡,适用于不同的应用场景。
目标
本项目的目标是加速FLUTE算法。我们提供了baseline.cpp可供使用,这是一个单线程程序。
运行方式
确保可执行文件的同目录下有POMV9.dat和PORT9.dat,这是FLUTE算法的查找表。运行时需要传入两个参数,分别是输入文件和输出文件。例如:
./flute data.in.bin data.out.bin数据格式
你可以使用datagen生成数据,也可以使用我们提供的数据进行测试。输入输出都是二进制格式,数据格式如下:
- 输入文件:
data.in.bin- 网络数量(num_nets):一个整数,表示网络的总数。
- 引脚起始索引(pin_st):一个整数数组,长度为num_nets + 1,表示每个网络的引脚在data_x和data_y数组中的起始位置。
- 引脚坐标(data_x 和 data_y):两个数组,分别存储所有引脚的x坐标和y坐标。
- 输出文件:
data.out.bin- 结果x坐标(result_x):一个数组,存储所有分支的x坐标。
- 结果y坐标(result_y):一个数组,存储所有分支的y坐标。
- 邻居节点索引(result_n):一个数组,存储每个分支的邻居节点索引。
附件中提供了一组参考输入输出文件,d1.in.bin与d1.out.bin。你也可以通过datagen.cpp直接生成测试文件。
运行环境
本题较为特殊,需要提交一个env文件指定运行环境,可选的环境如下:
intel:Intel 8358 CPU,16核心,24GB内存arm:Kunpeng 920 CPU,16核心,24GB内存cuda:NVIDIA L40 GPU,48G显存,附 4 核心 CPU,24GB内存npu:华为 Ascend 910B NPU,64G显存,附 20 核心 CPU,128GB内存。选手可用测试镜像crmirror.lcpu.dev/hpcgame/asend:ubuntu20.04。
评测标准
本题总分 200,采用分点评测的方式。
num_nets = 10000的测试点,只验证正确性,20分。
num_nets = 1000000的输入180分,设运行时长为T,评分规则如下:
- T大于 800s:不得分
- 20 < T <= 800:得分 = 450/(x-15)
- 14 < T <= 20:得分 = 90 + 15*(20-T)
- T <= 14:满分
提交内容
提交一个impl.cpp文件、以及选择的运行环境、自定义的编译选项(flags)
运行环境可以参考上文,自定义的编译选项可以为空,也可以指定编译选项,例如-O2。
最终我们运行的编译命令是:
intel:icpx impl.cpp -o impl $(flags)arm:bisheng-clang++ impl.cpp -o impl $(flags)cuda:nvcc impl.cu -o impl -arch=sm_89 $(flags)npu:联系管理员,手工评测
开始想的主打intel(实质是因为华为npu不太敢写,然后cuda的L40半天pending)
先交baseline再在编译的flag里面加各种优化先骗个20分咯xD
在考虑优化,简单在main里面对循环加openmp的并行化,交上去,28分
后续思考能不能拉进去avx指令集做进一步的优化,然并卵,写不明白交上去就wa掉了。
借助ai?这么长的文本也没几个ai能处理的来
{"env":"intel","flags":"-O3 -march=native -ftree-vectorize -funroll-loops -mavx2 -ffast-math -qopenmp"}
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
#include <algorithm>
#include <cassert>
#include <omp.h>
using std::max;
using std::min;
typedef unsigned DTYPE;
typedef struct
{
DTYPE x, y; // starting point of the branch
int n; // index of neighbor
} Branch;
typedef struct
{
int deg; // degree
DTYPE length; // total wirelength
Branch *branch; // array of tree branches
} Tree;
// Major functions
void readLUT();
DTYPE flute_wl(int d, DTYPE x[], DTYPE y[], int acc);
//Macro: DTYPE flutes_wl(int d, DTYPE xs[], DTYPE ys[], int s[], int acc);
Tree flute(int d, DTYPE x[], DTYPE y[], int acc);
//Macro: Tree flutes(int d, DTYPE xs[], DTYPE ys[], int s[], int acc);
DTYPE wirelength(Tree t);
void printtree(Tree t);
#define POWVFILE "POWV9.dat" // LUT for POWV (Wirelength Vector)
#define PORTFILE "PORT9.dat" // LUT for PORT (Routing Tree)
#define D 9 // LUT is used for d <= D, D <= 9
#define FLUTEROUTING 1 // 1 to construct routing, 0 to estimate WL only
#define REMOVE_DUPLICATE_PIN 0 // Remove dup. pin for flute_wl() & flute()
#define ACCURACY 8 // Default accuracy is 8
//#define MAXD 2008840 // max. degree of a net that can be handled
#define MAXD 1000 // max. degree of a net that can be handled
// Other useful functions
DTYPE flutes_wl_LD(int d, DTYPE xs[], DTYPE ys[], int s[]);
DTYPE flutes_wl_MD(int d, DTYPE xs[], DTYPE ys[], int s[], int acc);
DTYPE flutes_wl_RDP(int d, DTYPE xs[], DTYPE ys[], int s[], int acc);
Tree flutes_LD(int d, DTYPE xs[], DTYPE ys[], int s[]);
Tree flutes_MD(int d, DTYPE xs[], DTYPE ys[], int s[], int acc);
Tree flutes_RDP(int d, DTYPE xs[], DTYPE ys[], int s[], int acc);
#if REMOVE_DUPLICATE_PIN==1
#else
#define flutes_wl(d, xs, ys, s, acc) flutes_wl_ALLD(d, xs, ys, s, acc)
#define flutes(d, xs, ys, s, acc) flutes_ALLD(d, xs, ys, s, acc)
#endif
#define flutes_wl_ALLD(d, xs, ys, s, acc) flutes_wl_LMD(d, xs, ys, s, acc)
#define flutes_ALLD(d, xs, ys, s, acc) flutes_LMD(d, xs, ys, s, acc)
#define flutes_wl_LMD(d, xs, ys, s, acc) \
(d<=D ? flutes_wl_LD(d, xs, ys, s) : flutes_wl_MD(d, xs, ys, s, acc))
#define flutes_LMD(d, xs, ys, s, acc) \
(d<=D ? flutes_LD(d, xs, ys, s) : flutes_MD(d, xs, ys, s, acc))
#define ADIFF(x,y) ((x)>(y)?(x-y):(y-x)) // Absolute difference
#if D<=7
#elif D==8
#elif D==9
#define MGROUP 362880/4 // Max. # of groups, 9! = 362880
#define MPOWV 79 // Max. # of POWVs per group
#endif
int numgrp[10]={0,0,0,0,6,30,180,1260,10080,90720};
typedef struct point {
DTYPE x, y;
int o; //ZZ: temporarily store discretized x value indices
} POINT;
typedef POINT* POINTptr;
struct csoln
{
unsigned char parent;
unsigned char seg[12]; // Add: 0..i, Sub: j..11; seg[i+1]=seg[j-1]=0
unsigned char row[D-2], col[D-2];
unsigned char neighbor[2*D-2];
};
struct csoln *LUT[D+1][MGROUP]; // storing 4 .. D
int numsoln[D+1][MGROUP];
void readLUT();
Tree flute(int d, DTYPE x[], DTYPE y[], int acc);
Tree flutes_LD(int d, DTYPE xs[], DTYPE ys[], int s[]);
Tree flutes_MD(int d, DTYPE xs[], DTYPE ys[], int s[], int acc);
Tree flutes_RDP(int d, DTYPE xs[], DTYPE ys[], int s[], int acc);
Tree dmergetree(Tree t1, Tree t2);
Tree hmergetree(Tree t1, Tree t2, int s[]);
Tree vmergetree(Tree t1, Tree t2);
void printtree(Tree t);
void readLUT()
{
static bool LUTread = false;
if(LUTread) return;
LUTread = true;
FILE *fpwv, *fprt;
struct csoln *p;
int d, i, j, k, kk, ns, nn, ne;
unsigned char line[99], *linep, c;
unsigned char charnum[256];
unsigned char divd[256], modd[256], div16[256], mod16[256], dsq;
for (i=0; i<=255; i++) {
if ('0'<=i && i<='9')
charnum[i] = i - '0';
else if (i>='A')
charnum[i] = i - 'A' + 10;
else // if (i=='$' || i=='\n' || ... )
charnum[i] = 0;
div16[i] = i/16;
mod16[i] = i%16;
}
fpwv=fopen(POWVFILE, "r");
if (fpwv == NULL) {
printf("Error in opening %s\n", POWVFILE);
printf("Please make sure %s and %s\n"
"are in the current working directory.\n", POWVFILE, PORTFILE);
exit(1);
}
#if FLUTEROUTING==1
fprt=fopen(PORTFILE, "r");
if (fprt == NULL) {
printf("Error in opening %s\n", PORTFILE);
printf("Please make sure %s and %s\n(found in the Flute directory of UMpack)\n"
"are in the current working directory.\n", POWVFILE, PORTFILE);
exit(1);
}
#endif
for (d=4; d<=D; d++) {
for (i=0; i<=255; i++) {
divd[i] = i/d;
modd[i] = i%d;
}
dsq=d*d;
fscanf(fpwv, "d=%d\n", &d);
#if FLUTEROUTING==1
fscanf(fprt, "d=%d\n", &d);
#endif
for (k=0; k<numgrp[d]; k++) {
ns = (int) charnum[fgetc(fpwv)];
if (ns==0) { // same as some previous group
fscanf(fpwv, "%d\n", &kk);
numsoln[d][k] = numsoln[d][kk];
LUT[d][k] = LUT[d][kk];
}
else {
fgetc(fpwv); // '\n'
numsoln[d][k] = ns;
p = (struct csoln*) malloc(ns*sizeof(struct csoln));
LUT[d][k] = p;
for (i=1; i<=ns; i++) {
linep = (unsigned char*)fgets((char*)line, 99, fpwv);
p->parent = charnum[*(linep++)];
j = 0;
while ((p->seg[j++] = charnum[*(linep++)]) != 0) ;
j = 10;
while ((p->seg[j--] = charnum[*(linep++)]) != 0) ;
#if FLUTEROUTING==1
nn = 2*d-2;
ne = 2*d-3;
fread(line, 1, d-2, fprt); linep=line;
for (j=d; j<nn; j++) {
c = *(linep++);
if (c >= dsq) {
c -= dsq;
p->neighbor[divd[c]] = j;
ne--;
}
p->row[j-d] = divd[c];
p->col[j-d] = modd[c];
p->neighbor[j] = j; // initialized
}
fread(line, 1, ne+1, fprt); linep=line; // last char = \n
for (j=0; j<ne; j++) {
c = *(linep++);
p->neighbor[div16[c]] = mod16[c];
}
#endif
p++;
}
}
}
}
}
static int compare_x(const void *a, const void *b) {
const POINT *pa = *(const POINTptr*)a;
const POINT *pb = *(const POINTptr*)b;
if (pa->x < pb->x) return -1;
if (pa->x > pb->x) return 1;
if (pa->y < pb->y) return -1;
if (pa->y > pb->y) return 1;
return (pa < pb) ? -1 : 1; // 确保稳定性
}
// 比较函数,用于按y排序ptp数组
static int compare_y(const void *a, const void *b) {
const POINT *pa = *(const POINTptr*)a;
const POINT *pb = *(const POINTptr*)b;
if (pa->y < pb->y) return -1;
if (pa->y > pb->y) return 1;
if (pa->x < pb->x) return -1;
if (pa->x > pb->x) return 1;
return (pa < pb) ? -1 : 1;
}
Tree flute(int d, DTYPE x[], DTYPE y[], int acc) {
unsigned allocateSize = MAXD;
if (d > MAXD) {
allocateSize = d + 1;
}
// 使用对齐的内存分配以提高SIMD效率
DTYPE *xs, *ys;
int *s;
POINT *pt;
POINTptr *ptp;
posix_memalign((void **)&xs, 64, sizeof(DTYPE) * allocateSize);
posix_memalign((void **)&ys, 64, sizeof(DTYPE) * allocateSize);
posix_memalign((void **)&s, 64, sizeof(int) * allocateSize);
pt = (POINT *)malloc(sizeof(POINT) * allocateSize);
ptp = (POINTptr *)malloc(sizeof(POINTptr) * allocateSize);
for (int i = 0; i < d; i++) {
pt[i].x = x[i];
pt[i].y = y[i];
ptp[i] = &pt[i];
}
// 使用快速排序按x排序
qsort(ptp, d, sizeof(POINTptr), compare_x);
// 使用SIMD填充xs数组
#pragma omp simd aligned(xs : 64)
for (int i = 0; i < d; i++) {
xs[i] = ptp[i]->x;
ptp[i]->o = i;
}
// 使用快速排序按y排序
qsort(ptp, d, sizeof(POINTptr), compare_y);
// 使用SIMD填充ys和s数组
#pragma omp simd aligned(ys, s : 64)
for (int i = 0; i < d; i++) {
ys[i] = ptp[i]->y;
s[i] = ptp[i]->o;
}
Tree t = flutes(d, xs, ys, s, acc);
// 释放内存
free(xs);
free(ys);
free(s);
free(pt);
free(ptp);
return t;
}
// xs[] and ys[] are coords in x and y in sorted order
// s[] is a list of nodes in increasing y direction
// if nodes are indexed in the order of increasing x coord
// i.e., s[i] = s_i in defined in paper
// The points are (xs[s[i]], ys[i]) for i=0..d-1
// or (xs[i], ys[si[i]]) for i=0..d-1
// ZZ: RDP denotes Remove Duplicate Pin, simple, like std::unique
Tree flutes_RDP(int d, DTYPE xs[], DTYPE ys[], int s[], int acc)
{
int i, j, ss;
for (i=0; i<d-1; i++) {
if (xs[s[i]]==xs[s[i+1]] && ys[i]==ys[i+1]) {
if (s[i] < s[i+1])
ss = s[i+1];
else {
ss = s[i];
s[i] = s[i+1];
}
for (j=i+2; j<d; j++) {
ys[j-1] = ys[j];
s[j-1] = s[j];
}
for (j=ss+1; j<d; j++)
xs[j-1] = xs[j];
for (j=0; j<=d-2; j++)
if (s[j] > ss) s[j]--;
i--;
d--;
}
}
return flutes_ALLD(d, xs, ys, s, acc);
}
// For low-degree, i.e., 2 <= d <= D
Tree flutes_LD(int d, DTYPE xs[], DTYPE ys[], int s[])
{
int k, pi, i, j;
struct csoln *rlist, *bestrlist;
DTYPE dd[2*D-2]; // 0..D-2 for v, D-1..2*D-3 for h
DTYPE minl, sum;
DTYPE l[MPOWV+1];
int hflip;
Tree t;
t.deg = d;
t.branch = (Branch *) malloc((2*d-2)*sizeof(Branch));
if (d == 2) {
// printf("s[0]=%d, s[1]=%d, xs[0,1]=[%u,%u], ys[0,1]=[%u,%u]\n",
// s[0], s[1], xs[0], xs[1], ys[0], ys[1]);
minl = xs[1]-xs[0]+ys[1]-ys[0];
t.branch[0].x = xs[s[0]];
t.branch[0].y = ys[0];
t.branch[0].n = 1;
t.branch[1].x = xs[s[1]];
t.branch[1].y = ys[1];
t.branch[1].n = 1;
}
else if (d == 3) {
minl = xs[2]-xs[0]+ys[2]-ys[0];
t.branch[0].x = xs[s[0]];
t.branch[0].y = ys[0];
t.branch[0].n = 3;
t.branch[1].x = xs[s[1]];
t.branch[1].y = ys[1];
t.branch[1].n = 3;
t.branch[2].x = xs[s[2]];
t.branch[2].y = ys[2];
t.branch[2].n = 3;
t.branch[3].x = xs[1];
t.branch[3].y = ys[1];
t.branch[3].n = 3;
}
else {
k = 0;
if (s[0] < s[2]) k++;
if (s[1] < s[2]) k++;
for (i=3; i<=d-1; i++) { // p0=0 always, skip i=1 for symmetry
pi = s[i];
for (j=d-1; j>i; j--)
if (s[j] < s[i])
pi--;
k = pi + (i+1)*k;
}
if (k < numgrp[d]) { // no horizontal flip
hflip = 0;
for (i=1; i<=d-3; i++) {
dd[i]=ys[i+1]-ys[i];
dd[d-1+i]=xs[i+1]-xs[i];
}
}
else {
hflip = 1;
k=2*numgrp[d]-1-k;
for (i=1; i<=d-3; i++) {
dd[i]=ys[i+1]-ys[i];
dd[d-1+i]=xs[d-1-i]-xs[d-2-i];
}
}
minl = l[0] = xs[d-1]-xs[0]+ys[d-1]-ys[0];
rlist = LUT[d][k];
for (i=0; rlist->seg[i]>0; i++)
minl += dd[rlist->seg[i]];
bestrlist = rlist;
l[1] = minl;
j = 2;
while (j <= numsoln[d][k]) {
rlist++;
sum = l[rlist->parent];
for (i=0; rlist->seg[i]>0; i++)
sum += dd[rlist->seg[i]];
for (i=10; rlist->seg[i]>0; i--)
sum -= dd[rlist->seg[i]];
if (sum < minl) {
minl = sum;
bestrlist = rlist;
}
l[j++] = sum;
}
t.branch[0].x = xs[s[0]];
t.branch[0].y = ys[0];
t.branch[1].x = xs[s[1]];
t.branch[1].y = ys[1];
for (i=2; i<d-2; i++) {
t.branch[i].x = xs[s[i]];
t.branch[i].y = ys[i];
t.branch[i].n = bestrlist->neighbor[i];
}
t.branch[d-2].x = xs[s[d-2]];
t.branch[d-2].y = ys[d-2];
t.branch[d-1].x = xs[s[d-1]];
t.branch[d-1].y = ys[d-1];
if (hflip) {
if (s[1] < s[0]) {
t.branch[0].n = bestrlist->neighbor[1];
t.branch[1].n = bestrlist->neighbor[0];
}
else {
t.branch[0].n = bestrlist->neighbor[0];
t.branch[1].n = bestrlist->neighbor[1];
}
if (s[d-1] < s[d-2]) {
t.branch[d-2].n = bestrlist->neighbor[d-1];
t.branch[d-1].n = bestrlist->neighbor[d-2];
}
else {
t.branch[d-2].n = bestrlist->neighbor[d-2];
t.branch[d-1].n = bestrlist->neighbor[d-1];
}
for (i=d; i<2*d-2; i++) {
t.branch[i].x = xs[d-1-bestrlist->col[i-d]];
t.branch[i].y = ys[bestrlist->row[i-d]];
t.branch[i].n = bestrlist->neighbor[i];
}
}
else { // !hflip
if (s[0] < s[1]) {
t.branch[0].n = bestrlist->neighbor[1];
t.branch[1].n = bestrlist->neighbor[0];
}
else {
t.branch[0].n = bestrlist->neighbor[0];
t.branch[1].n = bestrlist->neighbor[1];
}
if (s[d-2] < s[d-1]) {
t.branch[d-2].n = bestrlist->neighbor[d-1];
t.branch[d-1].n = bestrlist->neighbor[d-2];
}
else {
t.branch[d-2].n = bestrlist->neighbor[d-2];
t.branch[d-1].n = bestrlist->neighbor[d-1];
}
for (i=d; i<2*d-2; i++) {
t.branch[i].x = xs[bestrlist->col[i-d]];
t.branch[i].y = ys[bestrlist->row[i-d]];
t.branch[i].n = bestrlist->neighbor[i];
}
}
}
t.length = minl;
return t;
}
// For medium-degree, i.e., D+1 <= d <= D2
Tree flutes_MD(int d, DTYPE xs[], DTYPE ys[], int s[], int acc)
{
unsigned allocateSize = MAXD;
if (d > MAXD)
allocateSize = d+1;
DTYPE *x1 = (DTYPE*) malloc(sizeof(DTYPE)*allocateSize);
DTYPE *x2 = (DTYPE*) malloc(sizeof(DTYPE)*allocateSize);
DTYPE *y1 = (DTYPE*) malloc(sizeof(DTYPE)*allocateSize);
DTYPE *y2 = (DTYPE*) malloc(sizeof(DTYPE)*allocateSize);
int *si = (int*) malloc(sizeof(int)*allocateSize);
int *s1 = (int*) malloc(sizeof(int)*allocateSize);
int *s2 = (int*) malloc(sizeof(int)*allocateSize);
float *score = (float*) malloc(sizeof(float)*2*allocateSize);
float *penalty = (float*) malloc(sizeof(float)*allocateSize);
DTYPE *distx = (DTYPE*) malloc(sizeof(DTYPE)*allocateSize);
DTYPE *disty = (DTYPE*) malloc(sizeof(DTYPE)*allocateSize);
// DTYPE x1[MAXD], x2[MAXD], y1[MAXD], y2[MAXD];
// int si[MAXD], s1[MAXD], s2[MAXD];
// float score[2*MAXD], penalty[MAXD];
// DTYPE distx[MAXD], disty[MAXD];
float pnlty, dx, dy;
DTYPE ll, minl, coord1, coord2;
int i, r, p, maxbp, bestbp, bp, nbp, ub, lb, n1, n2, nn1, nn2, ms, newacc;
Tree t, t1, t2, bestt1, bestt2;
int mins, maxs, minsi, maxsi;
DTYPE xydiff;
#pragma omp simd
for(i = 0; i < (int)allocateSize; ++i) {
distx[i] = disty[i] = 0;
}
if (s[0] < s[d-1]) {
ms = max(s[0], s[1]);
for (i=2; i<=ms; i++)
ms = max(ms, s[i]);
if (ms <= d-3) {
for (i=0; i<=ms; i++) {
x1[i] = xs[i];
y1[i] = ys[i];
s1[i] = s[i];
}
x1[ms+1] = xs[ms];
y1[ms+1] = ys[ms];
s1[ms+1] = ms+1;
s2[0] = 0;
for (i=1; i<=d-1-ms; i++)
s2[i] = s[i+ms]-ms;
t1 = flutes_LMD(ms+2, x1, y1, s1, acc);
t2 = flutes_LMD(d-ms, xs+ms, ys+ms, s2, acc);
t = dmergetree(t1, t2);
free(t1.branch);
free(t2.branch);
free(x1);
free(x2);
free(y1);
free(y2);
free(si);
free(s1);
free(s2);
free(score);
free(penalty);
free(distx);
free(disty);
return t;
}
}
else { // (s[0] > s[d-1])
ms = min(s[0], s[1]);
for (i=2; i<=d-1-ms; i++)
ms = min(ms, s[i]);
if (ms >= 2) {
x1[0] = xs[ms];
y1[0] = ys[0];
s1[0] = s[0]-ms+1;
for (i=1; i<=d-1-ms; i++) {
x1[i] = xs[i+ms-1];
y1[i] = ys[i];
s1[i] = s[i]-ms+1;
}
x1[d-ms] = xs[d-1];
y1[d-ms] = ys[d-1-ms];
s1[d-ms] = 0;
s2[0] = ms;
for (i=1; i<=ms; i++)
s2[i] = s[i+d-1-ms];
t1 = flutes_LMD(d+1-ms, x1, y1, s1, acc);
t2 = flutes_LMD(ms+1, xs, ys+d-1-ms, s2, acc);
t = dmergetree(t1, t2);
free(t1.branch);
free(t2.branch);
free(x1);
free(x2);
free(y1);
free(y2);
free(si);
free(s1);
free(s2);
free(score);
free(penalty);
free(distx);
free(disty);
return t;
}
}
// Find inverse si[] of s[]
for (r=0; r<d; r++)
si[s[r]] = r;
// Determine breaking directions and positions dp[]
lb=max((d-acc)/5, 2);
ub=d-1-lb;
// Compute scores
#define AA 0.6 // 2.0*BB
#define BB 0.3
//#define CCC max(0.425-0.005*d-0.015*acc, 0.1)
//#define CCC max(0.43-0.005*d-0.01*acc, 0.1)
#define CCC max(0.41-0.005*d, 0.1)
#define DD 4.8
float DDD = DD/(d-1);
// Compute penalty[]
dx = CCC*(xs[d-2]-xs[1])/(d-3);
dy = CCC*(ys[d-2]-ys[1])/(d-3);
for (r = d/2, pnlty = 0; r>=2; r--, pnlty += dx)
penalty[r] = pnlty, penalty[d-1-r] = pnlty;
penalty[1] = pnlty, penalty[d-2] = pnlty;
penalty[0] = pnlty, penalty[d-1] = pnlty;
for (r = d/2-1, pnlty = dy; r>=2; r--, pnlty += dy)
penalty[s[r]] += pnlty, penalty[s[d-1-r]] += pnlty;
penalty[s[1]] += pnlty, penalty[s[d-2]] += pnlty;
penalty[s[0]] += pnlty, penalty[s[d-1]] += pnlty;
//#define CC 0.16
//#define v(r) ((r==0||r==1||r==d-2||r==d-1) ? d-3 : abs(d-1-r-r))
// for (r=0; r<d; r++)
// penalty[r] = v(r)*dx + v(si[r])*dy;
// Compute distx[], disty[]
xydiff = (xs[d-1] - xs[0]) - (ys[d-1] - ys[0]);
if (s[0] < s[1])
mins = s[0], maxs = s[1];
else mins = s[1], maxs = s[0];
if (si[0] < si[1])
minsi = si[0], maxsi = si[1];
else minsi = si[1], maxsi = si[0];
for (r=2; r<=ub; r++) {
if (s[r] < mins)
mins = s[r];
else if (s[r] > maxs)
maxs = s[r];
distx[r] = xs[maxs] - xs[mins];
if (si[r] < minsi)
minsi = si[r];
else if (si[r] > maxsi)
maxsi = si[r];
disty[r] = ys[maxsi] - ys[minsi] + xydiff;
}
if (s[d-2] < s[d-1])
mins = s[d-2], maxs = s[d-1];
else mins = s[d-1], maxs = s[d-2];
if (si[d-2] < si[d-1])
minsi = si[d-2], maxsi = si[d-1];
else minsi = si[d-1], maxsi = si[d-2];
#pragma omp simd
for (r=d-3; r>=lb; r--) {
if (s[r] < mins)
mins = s[r];
else if (s[r] > maxs)
maxs = s[r];
distx[r] += xs[maxs] - xs[mins];
if (si[r] < minsi)
minsi = si[r];
else if (si[r] > maxsi)
maxsi = si[r];
disty[r] += ys[maxsi] - ys[minsi];
}
nbp=0;
#pragma omp simd
for (r=lb; r<=ub; r++) {
if (si[r]<=1)
score[nbp] = (xs[r+1] - xs[r-1]) - penalty[r]
- AA*(ys[2]-ys[1]) - DDD*disty[r];
else if (si[r]>=d-2)
score[nbp] = (xs[r+1] - xs[r-1]) - penalty[r]
- AA*(ys[d-2]-ys[d-3]) - DDD*disty[r];
else score[nbp] = (xs[r+1] - xs[r-1]) - penalty[r]
- BB*(ys[si[r]+1]-ys[si[r]-1]) - DDD*disty[r];
nbp++;
if (s[r]<=1)
score[nbp] = (ys[r+1] - ys[r-1]) - penalty[s[r]]
- AA*(xs[2]-xs[1]) - DDD*distx[r];
else if (s[r]>=d-2)
score[nbp] = (ys[r+1] - ys[r-1]) - penalty[s[r]]
- AA*(xs[d-2]-xs[d-3]) - DDD*distx[r];
else score[nbp] = (ys[r+1] - ys[r-1]) - penalty[s[r]]
- BB*(xs[s[r]+1]-xs[s[r]-1]) - DDD*distx[r];
nbp++;
}
if (acc <= 3)
newacc = 1;
else {
newacc = acc/2;
if (acc >= nbp) acc = nbp-1;
}
minl = (DTYPE) INT_MAX;
bestt1.branch = bestt2.branch = NULL;
for (i=0; i<acc; i++) {
maxbp = 0;
for (bp=1; bp<nbp; bp++)
if (score[maxbp] < score[bp]) maxbp = bp;
score[maxbp] = -9e9f;
#define BreakPt(bp) ((bp)/2+lb)
#define BreakInX(bp) ((bp)%2==0)
p = BreakPt(maxbp);
// Breaking in p
if (BreakInX(maxbp)) { // break in x
n1 = n2 = 0;
for (r=0; r<d; r++) {
if (s[r] < p) {
s1[n1] = s[r];
y1[n1] = ys[r];
n1++;
}
else if (s[r] > p) {
s2[n2] = s[r]-p;
y2[n2] = ys[r];
n2++;
}
else { // if (s[r] == p) i.e., r = si[p]
s1[n1] = p; s2[n2] = 0;
y1[n1] = y2[n2] = ys[r];
nn1 = n1; nn2 = n2;
n1++; n2++;
}
}
t1 = flutes_LMD(p+1, xs, y1, s1, newacc);
t2 = flutes_LMD(d-p, xs+p, y2, s2, newacc);
ll = t1.length + t2.length;
coord1 = t1.branch[t1.branch[nn1].n].y;
coord2 = t2.branch[t2.branch[nn2].n].y;
if (t2.branch[nn2].y > max(coord1, coord2))
ll -= t2.branch[nn2].y - max(coord1, coord2);
else if (t2.branch[nn2].y < min(coord1, coord2))
ll -= min(coord1, coord2) - t2.branch[nn2].y;
}
else { // if (!BreakInX(maxbp))
n1 = n2 = 0;
for (r=0; r<d; r++) {
if (si[r] < p) {
s1[si[r]] = n1;
x1[n1] = xs[r];
n1++;
}
else if (si[r] > p) {
s2[si[r]-p] = n2;
x2[n2] = xs[r];
n2++;
}
else { // if (si[r] == p) i.e., r = s[p]
s1[p] = n1; s2[0] = n2;
x1[n1] = x2[n2] = xs[r];
n1++; n2++;
}
}
t1 = flutes_LMD(p+1, x1, ys, s1, newacc);
t2 = flutes_LMD(d-p, x2, ys+p, s2, newacc);
ll = t1.length + t2.length;
coord1 = t1.branch[t1.branch[p].n].x;
coord2 = t2.branch[t2.branch[0].n].x;
if (t2.branch[0].x > max(coord1, coord2))
ll -= t2.branch[0].x - max(coord1, coord2);
else if (t2.branch[0].x < min(coord1, coord2))
ll -= min(coord1, coord2) - t2.branch[0].x;
}
if (minl > ll) {
minl = ll;
free(bestt1.branch);
free(bestt2.branch);
bestt1 = t1;
bestt2 = t2;
bestbp = maxbp;
}
else {
free(t1.branch);
free(t2.branch);
}
}
if (BreakInX(bestbp))
t = hmergetree(bestt1, bestt2, s);
else t = vmergetree(bestt1, bestt2);
free(bestt1.branch);
free(bestt2.branch);
free(x1);
free(x2);
free(y1);
free(y2);
free(si);
free(s1);
free(s2);
free(score);
free(penalty);
free(distx);
free(disty);
return t;
}
Tree dmergetree(Tree t1, Tree t2)
{
int i, d, prev, curr, next, offset1, offset2;
Tree t;
t.deg = d = t1.deg + t2.deg - 2;
t.length = t1.length + t2.length;
t.branch = (Branch *) malloc((2*d-2)*sizeof(Branch));
offset1 = t2.deg-2;
offset2 = 2*t1.deg-4;
for (i=0; i<=t1.deg-2; i++) {
t.branch[i].x = t1.branch[i].x;
t.branch[i].y = t1.branch[i].y;
t.branch[i].n = t1.branch[i].n + offset1;
}
for (i=t1.deg-1; i<=d-1; i++) {
t.branch[i].x = t2.branch[i-t1.deg+2].x;
t.branch[i].y = t2.branch[i-t1.deg+2].y;
t.branch[i].n = t2.branch[i-t1.deg+2].n + offset2;
}
for (i=d; i<=d+t1.deg-3; i++) {
t.branch[i].x = t1.branch[i-offset1].x;
t.branch[i].y = t1.branch[i-offset1].y;
t.branch[i].n = t1.branch[i-offset1].n + offset1;
}
for (i=d+t1.deg-2; i<=2*d-3; i++) {
t.branch[i].x = t2.branch[i-offset2].x;
t.branch[i].y = t2.branch[i-offset2].y;
t.branch[i].n = t2.branch[i-offset2].n + offset2;
}
prev = t2.branch[0].n + offset2;
curr = t1.branch[t1.deg-1].n + offset1;
next = t.branch[curr].n;
while (curr != next) {
t.branch[curr].n = prev;
prev = curr;
curr = next;
next = t.branch[curr].n;
}
t.branch[curr].n = prev;
return t;
}
Tree hmergetree(Tree t1, Tree t2, int s[])
{
int i, prev, curr, next, extra, offset1, offset2;
int p, ii, n1, n2, nn1, nn2;
DTYPE coord1, coord2;
Tree t;
t.deg = t1.deg + t2.deg - 1;
t.length = t1.length + t2.length;
t.branch = (Branch *) malloc((2*t.deg-2)*sizeof(Branch));
offset1 = t2.deg-1;
offset2 = 2*t1.deg-3;
p = t1.deg - 1;
n1 = n2 = 0;
for (i=0; i<t.deg; i++) {
if (s[i] < p) {
t.branch[i].x = t1.branch[n1].x;
t.branch[i].y = t1.branch[n1].y;
t.branch[i].n = t1.branch[n1].n + offset1;
n1++;
}
else if (s[i] > p) {
t.branch[i].x = t2.branch[n2].x;
t.branch[i].y = t2.branch[n2].y;
t.branch[i].n = t2.branch[n2].n + offset2;
n2++;
}
else {
t.branch[i].x = t2.branch[n2].x;
t.branch[i].y = t2.branch[n2].y;
t.branch[i].n = t2.branch[n2].n + offset2;
nn1 = n1; nn2 = n2; ii = i;
n1++; n2++;
}
}
for (i=t.deg; i<=t.deg+t1.deg-3; i++) {
t.branch[i].x = t1.branch[i-offset1].x;
t.branch[i].y = t1.branch[i-offset1].y;
t.branch[i].n = t1.branch[i-offset1].n + offset1;
}
for (i=t.deg+t1.deg-2; i<=2*t.deg-4; i++) {
t.branch[i].x = t2.branch[i-offset2].x;
t.branch[i].y = t2.branch[i-offset2].y;
t.branch[i].n = t2.branch[i-offset2].n + offset2;
}
extra = 2*t.deg-3;
coord1 = t1.branch[t1.branch[nn1].n].y;
coord2 = t2.branch[t2.branch[nn2].n].y;
if (t2.branch[nn2].y > max(coord1, coord2)) {
t.branch[extra].y = max(coord1, coord2);
t.length -= t2.branch[nn2].y - t.branch[extra].y;
}
else if (t2.branch[nn2].y < min(coord1, coord2)) {
t.branch[extra].y = min(coord1, coord2);
t.length -= t.branch[extra].y - t2.branch[nn2].y;
}
else t.branch[extra].y = t2.branch[nn2].y;
t.branch[extra].x = t2.branch[nn2].x;
t.branch[extra].n = t.branch[ii].n;
t.branch[ii].n = extra;
prev = extra;
curr = t1.branch[nn1].n + offset1;
next = t.branch[curr].n;
while (curr != next) {
t.branch[curr].n = prev;
prev = curr;
curr = next;
next = t.branch[curr].n;
}
t.branch[curr].n = prev;
return t;
}
Tree vmergetree(Tree t1, Tree t2)
{
int i, prev, curr, next, extra, offset1, offset2;
DTYPE coord1, coord2;
Tree t;
t.deg = t1.deg + t2.deg - 1;
t.length = t1.length + t2.length;
t.branch = (Branch *) malloc((2*t.deg-2)*sizeof(Branch));
offset1 = t2.deg-1;
offset2 = 2*t1.deg-3;
for (i=0; i<=t1.deg-2; i++) {
t.branch[i].x = t1.branch[i].x;
t.branch[i].y = t1.branch[i].y;
t.branch[i].n = t1.branch[i].n + offset1;
}
for (i=t1.deg-1; i<=t.deg-1; i++) {
t.branch[i].x = t2.branch[i-t1.deg+1].x;
t.branch[i].y = t2.branch[i-t1.deg+1].y;
t.branch[i].n = t2.branch[i-t1.deg+1].n + offset2;
}
for (i=t.deg; i<=t.deg+t1.deg-3; i++) {
t.branch[i].x = t1.branch[i-offset1].x;
t.branch[i].y = t1.branch[i-offset1].y;
t.branch[i].n = t1.branch[i-offset1].n + offset1;
}
for (i=t.deg+t1.deg-2; i<=2*t.deg-4; i++) {
t.branch[i].x = t2.branch[i-offset2].x;
t.branch[i].y = t2.branch[i-offset2].y;
t.branch[i].n = t2.branch[i-offset2].n + offset2;
}
extra = 2*t.deg-3;
coord1 = t1.branch[t1.branch[t1.deg-1].n].x;
coord2 = t2.branch[t2.branch[0].n].x;
if (t2.branch[0].x > max(coord1, coord2)) {
t.branch[extra].x = max(coord1, coord2);
t.length -= t2.branch[0].x - t.branch[extra].x;
}
else if (t2.branch[0].x < min(coord1, coord2)) {
t.branch[extra].x = min(coord1, coord2);
t.length -= t.branch[extra].x - t2.branch[0].x;
}
else t.branch[extra].x = t2.branch[0].x;
t.branch[extra].y = t2.branch[0].y;
t.branch[extra].n = t.branch[t1.deg-1].n;
t.branch[t1.deg-1].n = extra;
prev = extra;
curr = t1.branch[t1.deg-1].n + offset1;
next = t.branch[curr].n;
while (curr != next) {
t.branch[curr].n = prev;
prev = curr;
curr = next;
next = t.branch[curr].n;
}
t.branch[curr].n = prev;
return t;
}
int main(int argc, const char **argv) {
if(argc != 3) {
printf("usage: %s <input.bin> <output.bin>\n", argv[0]);
return 255;
}
readLUT();
FILE *input_fp = fopen(argv[1], "rb");
assert(input_fp);
fseek(input_fp, 0, SEEK_END);
unsigned long input_bin_size = ftell(input_fp);
fseek(input_fp, 0, SEEK_SET);
int *buf_input = (int *)malloc(input_bin_size);
assert(fread(buf_input, 1, input_bin_size, input_fp) == input_bin_size);
fclose(input_fp);
int num_nets = buf_input[0];
int *pin_st = buf_input + 1;
int tot_num_pins = pin_st[num_nets];
DTYPE *data_x = (DTYPE *)(pin_st + num_nets + 1);
DTYPE *data_y = (DTYPE *)(data_x + tot_num_pins);
DTYPE *result_x = (DTYPE *)calloc(tot_num_pins * 2, sizeof(DTYPE));
DTYPE *result_y = (DTYPE *)calloc(tot_num_pins * 2, sizeof(DTYPE));
int *result_n = (int *)calloc(tot_num_pins * 2, sizeof(int));
#pragma omp parallel for
for(int net_i = 0; net_i < num_nets; ++net_i) {
Tree t = flute(pin_st[net_i + 1] - pin_st[net_i],
data_x + pin_st[net_i],
data_y + pin_st[net_i],
ACCURACY);
// printf("%d %d\n", t.deg, t.length);
// for(int i = 0; i < 2 * t.deg - 2; ++i) {
// printf("%d %d %d\n", t.branch[i].x, t.branch[i].y, t.branch[i].n);
// }
int offset = pin_st[net_i] * 2;
for(int i = 0; i < 2 * t.deg - 2; ++i) {
result_x[offset + i] = t.branch[i].x;
result_y[offset + i] = t.branch[i].y;
result_n[offset + i] = t.branch[i].n;
}
free(t.branch);
}
FILE *output_fp = fopen(argv[2], "wb");
assert(output_fp);
fwrite(result_x, sizeof(DTYPE), tot_num_pins, output_fp);
fwrite(result_y, sizeof(DTYPE), tot_num_pins, output_fp);
fwrite(result_n, sizeof(int), tot_num_pins, output_fp);
fclose(output_fp);
free(result_x);
free(result_y);
free(result_n);
free(buf_input);
return 0;
}
文章评论