记录模板题：图论-树：最近公共祖先（LCA）

2025年4月9日 10点热度 0人点赞 0条评论

模板题：洛谷p3379

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入格式

第一行包含三个正整数 N,M,SN,M,S，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来 N−1N−1 行每行包含两个正整数 x,yx,y，表示 xx 结点和 yy 结点之间有一条直接连接的边（数据保证可以构成树）。

接下来 MM 行每行包含两个正整数 a,ba,b，表示询问 aa 结点和 bb 结点的最近公共祖先。

输出格式

输出包含 MM 行，每行包含一个正整数，依次为每一个询问的结果。

输入输出样例

输入 #1

输出 #1

说明/提示

对于 30%30% 的数据，N≤10N≤10，M≤10M≤10。

对于 70%70% 的数据，N≤10000N≤10000，M≤10000M≤10000。

对于 100%100% 的数据，1≤N,M≤5000001≤N,M≤500000，1≤x,y,a,b≤N1≤x,y,a,b≤N，不保证 a≠ba=b。

样例说明：

该树结构如下：

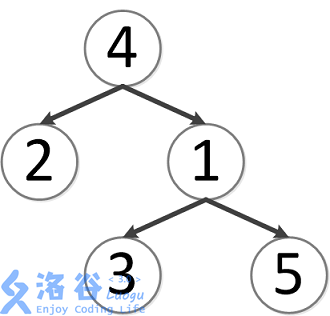
第一次询问：2,42,4 的最近公共祖先，故为 44。

第二次询问：3,23,2 的最近公共祖先，故为 44。

第三次询问：3,53,5 的最近公共祖先，故为 11。

第四次询问：1,21,2 的最近公共祖先，故为 44。

第五次询问：4,54,5 的最近公共祖先，故为 44。

故输出依次为 4,4,1,4,44,4,1,4,4。

2021/10/4 数据更新 @fstqwq：应要求加了两组数据卡掉了暴力跳。

一个经典的思想就是倍增法去解决，那什么是倍增算法呢？

思路很快就有了，但是要落实到代码上是另外一回事儿

首先要把树输入进去，在C++中一个经典的思路就是利用vector把两个邻边打进去就能轻松解决

然后开一个lg数组，初始化好2^i的数，根据题目就能轻松判断出只要父节点的数组开到22就好。

那么如何初始化2^i呢？

for(int i=1;i<=N;i++){
  lg[i]=lg[i-1];//先令lg[i]为上一个计算好的lg[i-1]
  if(i==1<<lg[i-1])lg[i]++;//i==1<<lg[i-1]这里的意思是如果i等于2的lg[n-1]次方的话，lg[i]加一
}

这样就把记录2^i的数组lg[i]初始化好了。

然后就是把整棵树遍历，将每个节点的深度和父节点记录下来，开一个表示深度的数组de和表示父节点的数组fa

//dfs遍历
void dfs(int u,int v){
    de[u]=de[v]+1;
    fa[u][0]=v;//2的0次方是1，也就是向上走一步就是u的父亲v
    //(1<<i)<=de[u]意思是当2^i小于节点u的深度的时候
    for(int i=1;(1<<i)<=de[u];i++){
        //简单的状态转移方程:节点 u 的第 2^i 层祖先，等于节点 u 的第 2^(i-1) 层祖先的第 2^(i-1) 层祖先。
        fa[u][i]=fa[fa[u][i-1]][i-1];
    }
    //注意:i对应第2^i层 层数=1,2,4,8,...... 设k=2^i
    //u的上k层祖先即为u的上k/2个祖先的第k/2个祖先且k%2=0（因为k=2^i）（雾） 
    //例如u的上4层祖先为上2层祖先的上2层祖先
    for(int i=0;i<g[u].size();i++){
        if(g[u][i]!=v)dfs(g[u][i],u);//没有遍历完就接着走下一层遍历
    }
}

接下来是开始进行lca函数，把两个节点的lca给整出来

C++

//最近公共祖先
int lca(int x,int y){
    if(de[x]<de[y])swap(x,y);//保证x深于y
    while(de[x]!=de[y])x=fa[x][lg[de[x]-de[y]]-1];//如果深度不同的时候，让x节点和y节点在同一深度上
    //lg[dep[x]-dep[y]]表示log(dep[x]-dep[y])+1,再减去1 
    //让x往上跳2^log([dep[x]-dep[y])层 
    /*
    倍增
    是不是任何一个正整数都能被一些2的n次方加起来?
    答案是:可以的，因为每个数字都可以用二进制表示 
    十进制：16=16        15=8+4+2+1          10=8+2        5=4+1            ...
    二进制：10000=10000  1111=1000+100+10+1  1010=1000+10  101=100+1        ...
    所以倍增LCA的意思就是: 每次以2的k次方跳跃!!
 
    （以上大致改编于arfa大佬的 
    [博客](https://www.luogu.org/blog/acking/solution-p3379)）
    
    这里就要用到lg数组判断x要往上跳多少 
    Q1：为什么要一步一步以2的k次方跳跃？ 
    因为fa[x][k]表示的是x的2^N层上的祖先,所以不能一步跳到上k（k为任意数）层的
    让x往上跳(2^k1+2^k2+2^k3+......)层 才能让x和y达到同一高度
    Q2：为什么x可以一步一步跳上y那一层？ 
    设 k=log([dep[x]-dep[y]) 
    k是向下取整，例如dep[x]-dep[y]=5=(101)2=(100)2+(1)2（二进制表示） 
    那么就要往上跳2次，分别跳 (100)2 、 (1)2 层 
    （所以，log(x)也可以表示x二进制除了最高位的1之外都去掉的形式） 
    往上跳了一次以后，dep[x]-dep[y]=(101)2-(100)2=(1)2，再往上跳(1)2层就可以了 
    x一步一步逼近y那一层，dep[x]-dep[y]一步一步减小，就能达到了 
    */
    if(x==y)return x;
    //如果`x和y是同一点的话,说明这个y本来就是x的祖先,所以直接返回`x
    for(int k=lg[de[x]]; k>=0; k--)
        if(fa[x][k]!=fa[y][k])
            x=fa[x][k],y=fa[y][k];
    //注意:层数=......,8,4,2,1 设p=2^k
    //如果`x的上p层的祖先的爸爸还是和`y的上p层的祖先的爸爸不一致
    //那么就让ta们往上爬p层
    return fa[x][0];//返回`x的爸爸(lca)
}

最后完整的代码：

#include<bits/stdc++.h>
using namespace std;
int N,M,S;
const int MAX_N=5e6+9;
vector<int>g[MAX_N];
int lg[MAX_N];
//lg[i]的定义:log(i)+1
int fa[MAX_N][22],de[MAX_N];//倍增法，fa[i][k]表示节点i走2^k层的祖先是哪个点
//最近公共祖先
int lca(int x,int y){
    if(de[x]<de[y])swap(x,y);//保证x深于y
    while(de[x]!=de[y])x=fa[x][lg[de[x]-de[y]]-1];//如果深度不同的时候，让x节点和y节点在同一深度上
    //lg[dep[x]-dep[y]]表示log(dep[x]-dep[y])+1,再减去1 
    //让x往上跳2^log([dep[x]-dep[y])层 
    /*
    倍增
    是不是任何一个正整数都能被一些2的n次方加起来?
    答案是:可以的，因为每个数字都可以用二进制表示 
    十进制：16=16        15=8+4+2+1          10=8+2        5=4+1            ...
    二进制：10000=10000  1111=1000+100+10+1  1010=1000+10  101=100+1        ...
    所以倍增LCA的意思就是: 每次以2的k次方跳跃!!
 
    （以上大致改编于arfa大佬的 
    [博客](https://www.luogu.org/blog/acking/solution-p3379)）
    
    这里就要用到lg数组判断x要往上跳多少 
    Q1：为什么要一步一步以2的k次方跳跃？ 
    因为fa[x][k]表示的是x的2^N层上的祖先,所以不能一步跳到上k（k为任意数）层的
    让x往上跳(2^k1+2^k2+2^k3+......)层 才能让x和y达到同一高度
    Q2：为什么x可以一步一步跳上y那一层？ 
    设 k=log([dep[x]-dep[y]) 
    k是向下取整，例如dep[x]-dep[y]=5=(101)2=(100)2+(1)2（二进制表示） 
    那么就要往上跳2次，分别跳 (100)2 、 (1)2 层 
    （所以，log(x)也可以表示x二进制除了最高位的1之外都去掉的形式） 
    往上跳了一次以后，dep[x]-dep[y]=(101)2-(100)2=(1)2，再往上跳(1)2层就可以了 
    x一步一步逼近y那一层，dep[x]-dep[y]一步一步减小，就能达到了 
    */
    if(x==y)return x;
    //如果`x和y是同一点的话,说明这个y本来就是x的祖先,所以直接返回`x
    for(int k=lg[de[x]]; k>=0; k--)
        if(fa[x][k]!=fa[y][k])
            x=fa[x][k],y=fa[y][k];
    //注意:层数=......,8,4,2,1 设p=2^k
    //如果`x的上p层的祖先的爸爸还是和`y的上p层的祖先的爸爸不一致
    //那么就让ta们往上爬p层
    return fa[x][0];//返回`x的爸爸(lca)
}
//dfs遍历
void dfs(int u,int v){
    de[u]=de[v]+1;
    fa[u][0]=v;//2的0次方是1，也就是向上走一步就是u的父亲v
    //(1<<i)<=de[u]意思是当2^i小于节点u的深度的时候
    for(int i=1;(1<<i)<=de[u];i++){
        //简单的状态转移方程:节点 u 的第 2^i 层祖先，等于节点 u 的第 2^(i-1) 层祖先的第 2^(i-1) 层祖先。
        fa[u][i]=fa[fa[u][i-1]][i-1];
    }
    //注意:i对应第2^i层 层数=1,2,4,8,...... 设k=2^i
    //u的上k层祖先即为u的上k/2个祖先的第k/2个祖先且k%2=0（因为k=2^i）（雾） 
    //例如u的上4层祖先为上2层祖先的上2层祖先
    for(int i=0;i<g[u].size();i++){
        if(g[u][i]!=v)dfs(g[u][i],u);//没有遍历完就接着走下一层遍历
    }
}
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>N>>M>>S;
    //初始化lg数组
    /*当 i=1 的时候，i=1 的二进制是 1，1 << lg[i-1] 是 1 << 0 = 1，所以 lg[i] = lg[0] + 1 → 0+1=1？
    然后当 i=2，lg[i] 一开始等于 lg[1]=1，接着检查 2 == 1<<1 → 2 == 2，所以 lg[2] 变为 2。这是个合理的 log2 实现，记录的是每个数的最大次方指数。 */
    for(int i=1;i<=N;i++){
        lg[i]=lg[i-1];//先令lg[i]为上一个计算好的lg[i-1]
        if(i==1<<lg[i-1])lg[i]++;
    }
    for(int i=0;i<N-1;i++){
        int x,y;
        cin>>x>>y;
        g[x].push_back(y);
        g[y].push_back(x);
    }
    //遍历整棵树，拉出来每个节点的深度
    dfs(S,0);//传入根节点和深度
    for(int i=0; i<M; i++) {
        int x,y;
        cin>>x>>y;
        cout<<lca(x,y)<<endl;
    }
    return 0;
}