C++ 标准库中实现了前缀和函数 std::partial_sum,定义于头文件 <numeric> 中。
一个经典的例题:

暴力当然直接TLE
//这段代码是能拿50分的,大规模会有超时问题
//没有很好的利用前缀和
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
vector<int>a;
for(int i=0;i<n;i++){
int t;cin>>t;
a.push_back(t);
}
int m;
cin>>m;
for(int i=0;i<m;i++){
int l,r,t=0;
cin>>l>>r;
for(int j=l-1;j<=r-1;j++)t+=a[j];
cout<<t<<endl;
}
return 0;
}将上面代码的加起来的过程给优化一下,在输入阶段就将数组改写成前缀和的形式,输出的时候只要s[r]-s[l-1]就可以了
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
vector<int>a;a.push_back(0);
for(int i=1;i<=n;i++){
int t;cin>>t;
a.push_back(t+a[i-1]);
}
int m;cin>>m;
for(int i=0;i<m;i++){
int l,r;
cin>>l>>r;
cout<<a[r]-a[l-1]<<endl;
}
return 0;
}从一维扩展到二维,思考方式就多了
一个是基于容斥原理,什么是容斥原理?这涉及到数学上集合的概念了。先看下面的图:
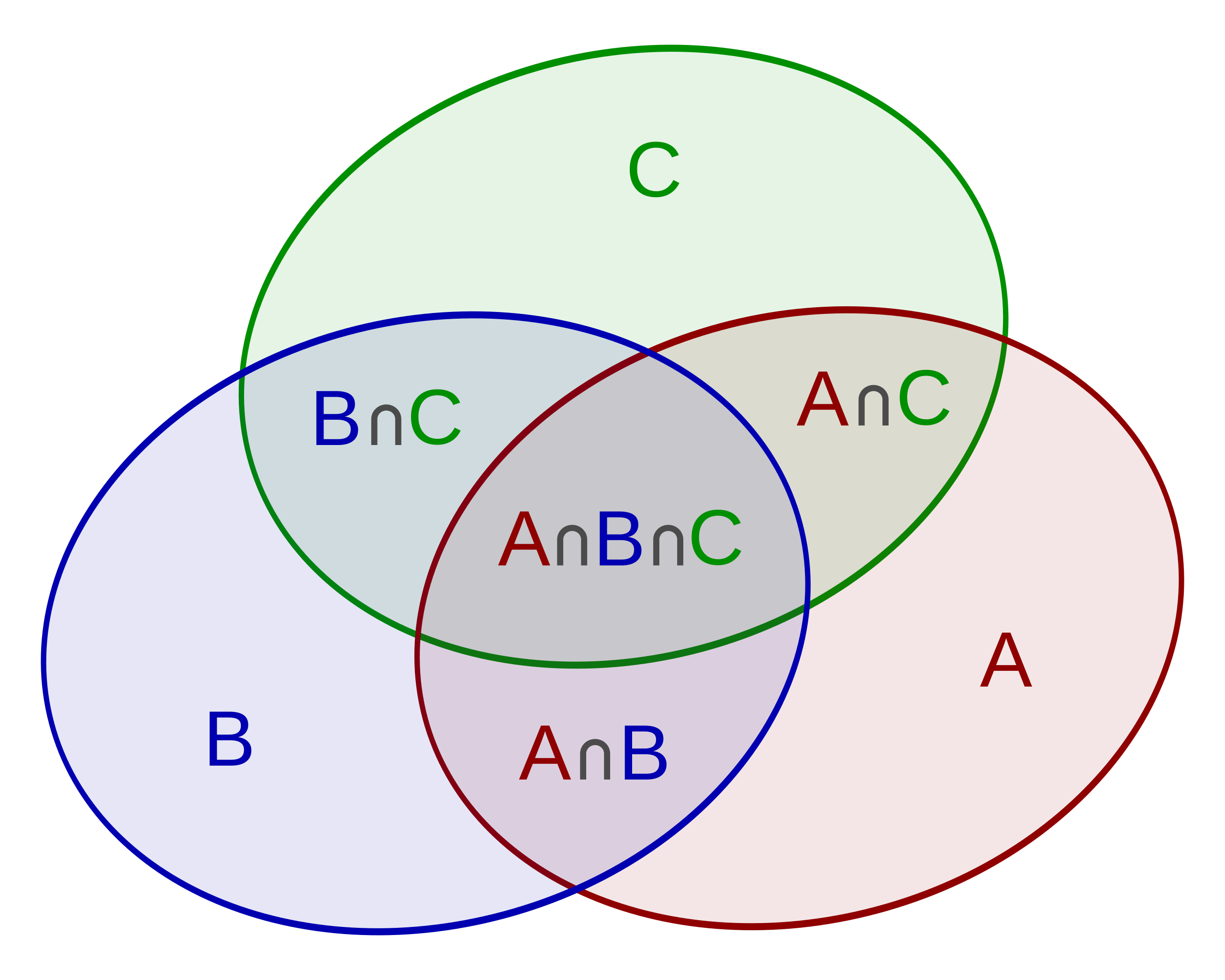
现在给了A,B,C三个集合的元素数量,要求你求出至少在一个元素的数量,他不能是直接把三个集合的元素加起来,必须得把重复的元素给扣掉,计算这个数量的过程就是容斥原理。
现在回到二维前缀和的部分,给定大小为 m *n 的二维数组 A,要求出其前缀和 S。那么,S 同样是大小为 m* n 的二维数组,且
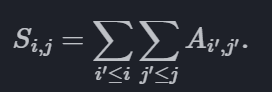
类比一维的情形,S{i,j} 应该可以基于 S{i-1,j} 或 S{i,j-1} 计算,从而避免重复计算前面若干项的和。但是,如果直接将 S{i-1,j} 和 S{i,j-1} 相加,再加上 A{i,j},会导致重复计算 S{i-1,j-1} 这一重叠部分的前缀和,所以还需要再将这部分减掉。这就符合了容斥原理。由此得到如下递推关系:
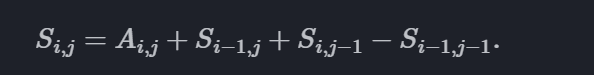
实现时,直接遍历 (i,j) 求和即可。

同样的道理,在已经预处理出二位前缀和后,要查询左上角为 (i[1],j[1])、右下角为 (i[2],j[2]) 的子矩阵的和,可以计算
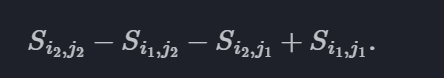
这可以在 O(1) 时间内完成。
在二维的情形,以上算法的时间复杂度可以简单认为是 O(mn),即与给定数组的大小成线性关系。但是,当维度 k 增大时,由于容斥原理涉及的项数以指数级的速度增长,时间复杂度会成为 O(2^kN),这里 k 是数组维度,而 N 是给定数组大小。因此,该算法不再适用。
接下来是差分:
差分的定义:在多张图画中,主体结构不变,展现其他较小变化的多张图片,可称其互为差分。
在算法中,他是一种和前缀和相对的策略
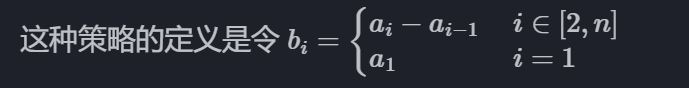
这里的a[i]即数组中每个元素

它可以维护多次对序列的一个区间加上一个数,并在最后询问某一位的数或是多次询问某一位的数。注意修改操作一定要在查询操作之前。

例题:
 思路
思路
这题明显就是差分
根据差分数组的定义: d[i]=a[i]-a[i-1],可以发现,在d[x]上加上z,会让后面的学生全部加上z。↓

但这是把后面全部都加了,还要减掉一节,所以↓

把两个综合起来就是↓

所以每一次变化只要把d[x]+z,d[y+1]-z就好了。
因为 d[i]=a[i]-a[i-1]
所以 a[i-1]+d[i]=a[i]
最后再根据 a[i-1]+d[i]=a[i]输出每一个同学的分数
题解:
#include<bits/stdc++.h>
using namespace std;
int main(){
int n,p;
cin>>n>>p;
vector<int>a(n+1,0),d(n+1,0);//动态分配内存的数组
for(int i=1;i<=n;i++){
cin>>a[i];
d[i]=a[i]-a[i-1];//差分
}
int x,y,z;
for(int i=0;i<p;i++){
cin>>x>>y>>z;
d[x]+=z,d[y+1]-=z;
}
int min=300;
//找出分数最少的学生
for(int i=1;i<=n;i++){
a[i]=a[i-1]+d[i];
if(min>a[i])min=a[i];
}
//经过上面的操作,将时间复杂度给干到O(n)了
cout<<min<<endl;
return 0;
}
文章评论